题目内容
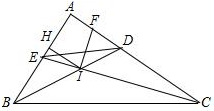 如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,IH⊥AB于H,下列结论:①∠DIF=45°;②CF+BE=BC;③AE+AF=2AH;④S四边形△BEDC=2S△IBC,其中正确结论的个数为( )
如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,IH⊥AB于H,下列结论:①∠DIF=45°;②CF+BE=BC;③AE+AF=2AH;④S四边形△BEDC=2S△IBC,其中正确结论的个数为( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:角平分线的性质
专题:
分析:由条件可知I为△ABC的内切圆的圆心,设与BC、AC两边分别切于点J、G,连接IJ、IG,则可知IG⊥AC,IJ⊥BC,利用三角形内角和及角平分线的定义可求得∠BIC=135°,可求得∠CID=45°,则可得出①正确;可证明△IGD≌△IHE,则可判断②③正确;利用切线长定理可得△BIE≌△BIJ,△CID≌△CIJ,可判断④不正确.
解答: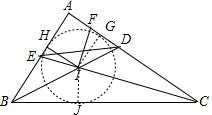 解:
解:
由题意可知I为△ABC内切圆的圆心,
如图,设与BC、AC两边分别切于点J、G,连接IJ、IG,则可知IG⊥AC,IJ⊥BC,
∵BI、CI平分∠ABC和∠ACB,
∴∠BIC=180°-∠IBJ-∠ICJ=180°-
(∠ABC+ACB)=180°-
(180°-∠A)=90°+
∠A=135°,
∴∠CID=45°,
∵FI⊥CE,
∴∠DIF=90°-∠CID=45°,
∴①正确;
∵∠A=90°,IH⊥AB,IG⊥AC,
∴∠HIG=90°,
∴∠HIE+∠HIF=∠HIF+∠FIG=90°,
∴∠HIE=∠FIG,
在△HIE和△GIF中
∴△HIE≌△GIF(ASA),
∴HE=GF,
又由切线长定理可知AH=AG,CG=CJ,BH=BJ,
∴AE+AF=AH+HE+AG-GF=2AH,CF+BE=CG+GF+BH-EH=CG+BH=BJ+CJ=BC,
∴②③正确;
且容易证明△BIE≌△BIJ,△CID≌△CIJ,
∴S△BIH=S△BIJ,S△CIG=S△CIJ,
∴S△BIC=S△BIH+S△CIG=S△BIE+S△HIE+S△CIF-S△GIF=S△BIE+S△CIF,
∴S四边形BEDC=2S△BIC+S△DIE>2S△BIC,
∴④不正确;
综上可知正确的为①②③,共三个,
故选C.
 解:
解:由题意可知I为△ABC内切圆的圆心,
如图,设与BC、AC两边分别切于点J、G,连接IJ、IG,则可知IG⊥AC,IJ⊥BC,
∵BI、CI平分∠ABC和∠ACB,
∴∠BIC=180°-∠IBJ-∠ICJ=180°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CID=45°,
∵FI⊥CE,
∴∠DIF=90°-∠CID=45°,
∴①正确;
∵∠A=90°,IH⊥AB,IG⊥AC,
∴∠HIG=90°,
∴∠HIE+∠HIF=∠HIF+∠FIG=90°,
∴∠HIE=∠FIG,
在△HIE和△GIF中
|
∴△HIE≌△GIF(ASA),
∴HE=GF,
又由切线长定理可知AH=AG,CG=CJ,BH=BJ,
∴AE+AF=AH+HE+AG-GF=2AH,CF+BE=CG+GF+BH-EH=CG+BH=BJ+CJ=BC,
∴②③正确;
且容易证明△BIE≌△BIJ,△CID≌△CIJ,
∴S△BIH=S△BIJ,S△CIG=S△CIJ,
∴S△BIC=S△BIH+S△CIG=S△BIE+S△HIE+S△CIF-S△GIF=S△BIE+S△CIF,
∴S四边形BEDC=2S△BIC+S△DIE>2S△BIC,
∴④不正确;
综上可知正确的为①②③,共三个,
故选C.
点评:本题主要考查角平分线的性质及切线的性质,掌握三角形角平分线的交点为内切圆的圆心,从而画出内切圆是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,B处在A处的南偏西65°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,则∠ACB的度数是( )
如图,B处在A处的南偏西65°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,则∠ACB的度数是( )| A、80° | B、75° |
| C、85° | D、70° |
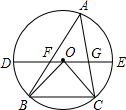 如图,△ABC为⊙O的内接三角形,∠A=60°,直径DE∥BC,AB、AC分别与DE相交于点F、G,若⊙O的半径为2,则线段FG的最大值为
如图,△ABC为⊙O的内接三角形,∠A=60°,直径DE∥BC,AB、AC分别与DE相交于点F、G,若⊙O的半径为2,则线段FG的最大值为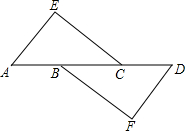 如图,∠A=∠D,AB=CD,要使△AEC≌△DFB,还需要补充一个条件,这个条件可以是
如图,∠A=∠D,AB=CD,要使△AEC≌△DFB,还需要补充一个条件,这个条件可以是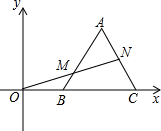 如图,平面直角坐标系内,正三角形ABC的顶点B,C的坐标分别为(2,0),(6,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为
如图,平面直角坐标系内,正三角形ABC的顶点B,C的坐标分别为(2,0),(6,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为