题目内容
一个圆锥的底面半径为3厘米，高为3
厘米．求圆锥轴截面中两母线所夹角的度数．
| 3 |
考点：圆锥的计算
专题：计算题
分析：如图，△ABC为圆锥的轴截面AO为圆锥的高，OB=OC=3，AO=3
，先利用勾股定理计算出AC=6，则AB=6，则可判断△ABC为等边三角形，所以∠BAC=60°．
| 3 |
解答：解：如图，△ABC为圆锥的轴截面，
AO为圆锥的高，
OB=OC=3，AO=3
，
在Rt△AOC中，AC=
=6，
所以AB=AC=6，
而BC=6，
所以△ABC为等边三角形，
所以∠BAC=60°，
即圆锥轴截面中两母线所夹角的度数为60°．
AO为圆锥的高，OB=OC=3，AO=3
| 3 |
在Rt△AOC中，AC=
| OC2+AO2 |
所以AB=AC=6，
而BC=6，
所以△ABC为等边三角形，
所以∠BAC=60°，
即圆锥轴截面中两母线所夹角的度数为60°．
点评：本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
下列说法错误的是（ ）
| A、近似数0.8与0.80表示的意义不同 |
| B、近似数2千万和2000万的精确度不一样 |
| C、3.450×104是精确到十位的近似数 |
| D、49554精确到万位是4.9×105 |
如图，已知AD是△ABC的角平分线，求证：
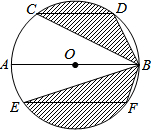如图，AB是⊙O的直径，CD、EF是⊙O的弦，且AB∥CD∥EF，AB=10，CD=6，EF=8．则图中阴影部分的面积为
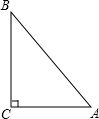已知：如图，Rt△ABC中，∠C=90°，AC=6，AB=10．