题目内容
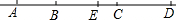 如图,B、C两点把线段AD分成2:3:4的三部分,点E是线段AD的中点,EC=2cm,求:
如图,B、C两点把线段AD分成2:3:4的三部分,点E是线段AD的中点,EC=2cm,求:(1)AD的长;
(2)AB:BE.
考点:两点间的距离
专题:
分析:(1)根据线段的比,可设出未知数,根据线段的和差,可得方程,根据解方程,可得x的值,根据x的值,可得AD的长度;
(2)根据线段的和差,可得线段BE的长,根据比的意义,可得答案.
(2)根据线段的和差,可得线段BE的长,根据比的意义,可得答案.
解答:解:(1)设AB=2x,则BC=3x,CD=4x,
由线段的和差,得AD=AB+BC+CD=9x.
由E为AD的中点,得
ED=
AD=
x.
由线段的和差,得
CE=DE-CD=
AD-CD=
x-4x=
x=2.
解得x=4.
∴AD=9x=36(cm),
(2)AB=2x=8,AE=
AD=18.
由线段的和差,得
BE=AE-AB=18-8=810(cm).
AB:BE=8:10=4:5.
由线段的和差,得AD=AB+BC+CD=9x.
由E为AD的中点,得
ED=
| 1 |
| 2 |
| 9 |
| 2 |
由线段的和差,得
CE=DE-CD=
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
解得x=4.
∴AD=9x=36(cm),
(2)AB=2x=8,AE=
| 1 |
| 2 |
由线段的和差,得
BE=AE-AB=18-8=810(cm).
AB:BE=8:10=4:5.
点评:本题考查了两点间的距离,利用了线段的和差,线段中点的性质,比的意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

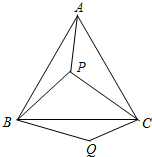 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.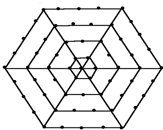 如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推. 延长线段AB是指按从端点A到B的方向延长;延长线段BA是指按从端点B到A的方向延长,这时也可以说成反向延长线段AB,如图,分别画出线段AB的延长线和反向延长线.
延长线段AB是指按从端点A到B的方向延长;延长线段BA是指按从端点B到A的方向延长,这时也可以说成反向延长线段AB,如图,分别画出线段AB的延长线和反向延长线.