题目内容
17.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°-∠B,④3∠A=2∠B=∠C中,能确定△ABC是直角三角形的条件有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据直角三角形的判定对各个条件进行分析,从而得到答案.
解答 解:①因为∠A+∠B=∠C,则2∠C=180°,∠C=90°,所以△ABC是直角三角形;
②因为∠A:∠B:∠C=1:2:3,设∠A=x,则x+2x+3x=180,x=30°,∠C=30°×3=90°,所以△ABC是直角三角形;
③因为∠A=90°-∠B,所以∠A+∠B=90°,则∠C=180°-90°=90°,所以△ABC是直角三角形;
④因为3∠A=2∠B=∠C,∠A+∠B+∠C=$\frac{1}{3}$∠C+$\frac{1}{2}$∠C+∠C=180°,∠C=$\frac{1080}{11}$°,所以三角形为钝角三角形.
所以能确定△ABC是直角三角形的有①②③共3个.
故选:C.
点评 此题考查三角形的内角和定理:三角形的内角和为180°;理解三角形内若有一个内角为90°,则△ABC是直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.把方程x2-4x-6=0配方,化为(x+m)2=n的形式应为( )
| A. | (x-4)2=6 | B. | (x-2)2=4 | C. | (x-2)2=0 | D. | (x-2)2=10 |
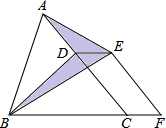 如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=5CF,四边形DCFE是平行四边形,则图中阴影部分的面积为6.
如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=5CF,四边形DCFE是平行四边形,则图中阴影部分的面积为6.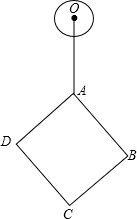 如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )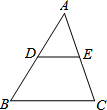 如图,DE是△ABC的中位线,若BC的长是12cm,则DE的长是6cm.
如图,DE是△ABC的中位线,若BC的长是12cm,则DE的长是6cm.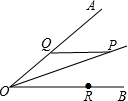 如图所示,∠AOB=30°,角内有点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长最小值是10.
如图所示,∠AOB=30°,角内有点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长最小值是10. 如图,已知点A,C在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,D在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是6.
如图,已知点A,C在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,D在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是6.