题目内容
根据一个三角形的内角情况判断三角形的形状,关键是利用三角形内角和定理求出各个角,再根据各类三角形的性质判断.
若有两个角相等,则可判定为 三角形;
若有三个角相等,则可判定为 三角形;
若特殊角90°和两个角45°,则为 三角形.
若有两个角相等,则可判定为
若有三个角相等,则可判定为
若特殊角90°和两个角45°,则为
考点:三角形内角和定理
专题:
分析:(1)根据有两个角相等的三角形为等腰三角形即可解题;
(2)三个角相等,根据内角和为180°,即可求得每个内角为60°,即可解题;
(3)根据等腰直角三角形的定义即可解题.
(2)三个角相等,根据内角和为180°,即可求得每个内角为60°,即可解题;
(3)根据等腰直角三角形的定义即可解题.
解答:解:(1)三角形中有两个角相等,则该三角形为等腰三角形;
(2)∵三个角相等,且三个角的和为180°,
∴每个角都为60°,
∴该三角形为等边三角形;
(3)∵有一个角为90°,∴该三角形为直角三角形,
∵两个角为45°,∴该三角形为等腰三角形,
∴该三角形为等腰直角三角形.
故答案为:等腰、等边、等腰直角.
(2)∵三个角相等,且三个角的和为180°,
∴每个角都为60°,
∴该三角形为等边三角形;
(3)∵有一个角为90°,∴该三角形为直角三角形,
∵两个角为45°,∴该三角形为等腰三角形,
∴该三角形为等腰直角三角形.
故答案为:等腰、等边、等腰直角.
点评:本题考查了三角形内角和为180°的性质,考查了等腰三角形、等边三角形、等腰直角三角形的判定.

练习册系列答案
相关题目
 如图,一个无盖的正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,蚂蚁爬行的最短距离是( )
如图,一个无盖的正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,蚂蚁爬行的最短距离是( )A、
| ||
B、
| ||
| C、1 | ||
D、2+
|
 如图,在正五边形ABCDE中,对角线AC,BD相交于点F.
如图,在正五边形ABCDE中,对角线AC,BD相交于点F.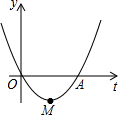 如图,抛物线y=x2+bx+c过原点,且与x轴交于A(4,0),M为抛物线的顶点,问抛物线是否存在点P,使得∠POM=90°?若存在,求出点P坐标;若不存在,说明理由.
如图,抛物线y=x2+bx+c过原点,且与x轴交于A(4,0),M为抛物线的顶点,问抛物线是否存在点P,使得∠POM=90°?若存在,求出点P坐标;若不存在,说明理由.