题目内容
 如图,在正五边形ABCDE中,对角线AC,BD相交于点F.
如图,在正五边形ABCDE中,对角线AC,BD相交于点F.(1)判断△ABF的形状,并说明理由;
(2)求证:四边形AFDE为菱形.
考点:正多边形和圆,菱形的判定
专题:
分析:(1)利用正五边形的性质求出各内角度数,进而利用等腰三角形的性质和判定得出答案.
(2)首先由正五边形的性质可得AB=BC=CD=DE=AE,BE∥CD,AD∥BC,AC∥DE,AC=AD=BE,根据有一组邻边相等的平行四边形是菱形即可证.
(2)首先由正五边形的性质可得AB=BC=CD=DE=AE,BE∥CD,AD∥BC,AC∥DE,AC=AD=BE,根据有一组邻边相等的平行四边形是菱形即可证.
解答:解:△ABF是等腰三角形,
理由是:∵在正五边形ABCDE中,对角线BD、AC交于F,
∴∠AED=∠EDC=∠BCD=108°,AC=BD,AE=DE,
∴∠BAC=∠CBD=36°,
∴∠ABD=∠ABC-∠CBD=108°-36°=72°;
∴∠AFB=180°-36°-72°=72°,
∴∠ABD=∠AFB,
∴△ABF为等腰三角形;
(2)证明:∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,BD∥AE,AC∥DE,
∴四边形DENC是平行四边形,
∵AE=AF,
∴四边形AFDE是菱形.
理由是:∵在正五边形ABCDE中,对角线BD、AC交于F,
∴∠AED=∠EDC=∠BCD=108°,AC=BD,AE=DE,
∴∠BAC=∠CBD=36°,
∴∠ABD=∠ABC-∠CBD=108°-36°=72°;
∴∠AFB=180°-36°-72°=72°,
∴∠ABD=∠AFB,
∴△ABF为等腰三角形;
(2)证明:∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,BD∥AE,AC∥DE,
∴四边形DENC是平行四边形,
∵AE=AF,
∴四边形AFDE是菱形.
点评:本题考查了正多边形的性质,利用正五边形的性质得出内角度数是解题关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
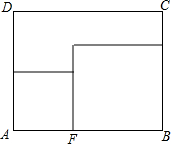 如图,矩形纸片ABCD,AD=8,AB=10,点F在AB上,分别以AF、FB为边裁出的两个小正方形纸片面积和S的取值范围是
如图,矩形纸片ABCD,AD=8,AB=10,点F在AB上,分别以AF、FB为边裁出的两个小正方形纸片面积和S的取值范围是 如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个半圆柱而成,中间可供滑行部分的横截面是半径为3m的半圆,该部分的边缘AB=CD=45m,点E在CD上,CE=5m,一滑行爱好者从A点到E点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取整数3)
如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个半圆柱而成,中间可供滑行部分的横截面是半径为3m的半圆,该部分的边缘AB=CD=45m,点E在CD上,CE=5m,一滑行爱好者从A点到E点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取整数3) 如图,圆O与四边形ABCD四边都相切,试讨论四边形ABCD边与边之间有何关系.
如图,圆O与四边形ABCD四边都相切,试讨论四边形ABCD边与边之间有何关系.