题目内容
 已知:在直角坐标系中,点A(-1,0),点B(3,0),点C在函数y=
已知:在直角坐标系中,点A(-1,0),点B(3,0),点C在函数y=| 2 |
| x |
考点:反比例函数综合题
专题:计算题
分析:过C作CD⊥AB,由A与B坐标确定出AB的长,由CA=AB,利用三线合一得到D为AB中点,求出AD的长,进而求出OD的长,即为C横坐标,代入反比例解析式求出纵坐标确定出C坐标,设M(0,-m),表示出直线MC解析式,确定出N坐标,由MC为角平分线,利用角平分线定理列出关系式,求出m的值,即可确定出M坐标.
解答: 解:过C作CD⊥AB,
解:过C作CD⊥AB,
∵CA=CB,A(-1,0),点B(3,0),即AB=4,
∴AD=BD=2,即OD=1,
把x=1代入y=
得:y=2,即C(1,2),
设M(0,-m),则直线MC解析式为y-2=
(x-1),即y=(m+2)x-m,
令y=0,得到x=
,即直线CM与直线AB交点为N(
,0),
由角平分线定理得:
=
,即
=
,
解得:m=
,
则M坐标为(0,-
).
 解:过C作CD⊥AB,
解:过C作CD⊥AB,∵CA=CB,A(-1,0),点B(3,0),即AB=4,
∴AD=BD=2,即OD=1,
把x=1代入y=
| 2 |
| x |
设M(0,-m),则直线MC解析式为y-2=
| 2+m |
| 1 |
令y=0,得到x=
| m |
| m+2 |
| m |
| m+2 |
由角平分线定理得:
| MA |
| MB |
| NA |
| NB |
| ||
|
| ||
3-
|
解得:m=
| 3 |
则M坐标为(0,-
| 3 |
点评:此题属于反比例函数综合题,涉及的知识有:直线的两点式方程,两点间的距离公式,角平分线定理,以及坐标与图形性质,熟练掌握角平分线定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四边形ABCD是一个平行四边形,△PAB的面积是7平方厘米,△PCD的面积是5平方厘米,求平行四边形ABCD的面积.
如图,四边形ABCD是一个平行四边形,△PAB的面积是7平方厘米,△PCD的面积是5平方厘米,求平行四边形ABCD的面积. 如图,在高4米的平房顶上A处望一栋楼的底部D时,视线恰好过树的顶端E,从平房底部B处望楼顶C时,视线也恰好过小树的顶端E.如果测出小树EF的高度为3米,那么你能推算出楼CD的高度吗?若能,请写出你的推算过程.
如图,在高4米的平房顶上A处望一栋楼的底部D时,视线恰好过树的顶端E,从平房底部B处望楼顶C时,视线也恰好过小树的顶端E.如果测出小树EF的高度为3米,那么你能推算出楼CD的高度吗?若能,请写出你的推算过程.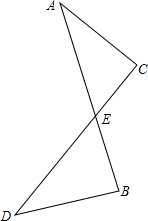 如图,已知AB与CD交于点E,AB与CD的夹角为45°,若∠B+∠C=225°,AC=3,DB=4,AB=5,求DC的长.
如图,已知AB与CD交于点E,AB与CD的夹角为45°,若∠B+∠C=225°,AC=3,DB=4,AB=5,求DC的长.