题目内容
4.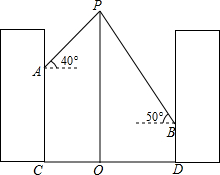 如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)
如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)
分析 过E作AE⊥OP于E,BF⊥OP于F,根据矩形的性质得到AC=8m,OE=8m,在Rt△AEP中,求得PE=8.5m,于是得到OP=16.5m;在Rt△BFP中,求得PF=11.9m,于是得到结论
解答 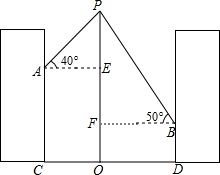 解:过E作AE⊥OP于E,BF⊥OP于F,
解:过E作AE⊥OP于E,BF⊥OP于F,
∵OC=OD=10m,AC=8m,
∴AE=BF=10m,OE=8m,
在Rt△AEP中,PE=AE•tan40°=10×0.85=8.5m,
∴OP=PE+OE=8.5+8=16.5m;
在Rt△BFP中,PF=BF•tan50°=10×1.19=11.9m,
∴BD=OF=OP-PF=4.6m,
答:旗秆OP的长度是16.5m,BD的长是4.6m.
点评 此题考查了解直角三角形的应用-仰角俯角问题,作出辅助线,构造直角三角形是解题的关键.

练习册系列答案
相关题目
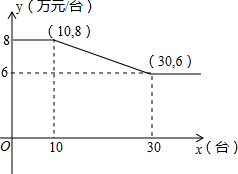 某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.
某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.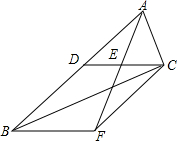 如图,四边形BFCD为平行四边形,点E是AF的中点.
如图,四边形BFCD为平行四边形,点E是AF的中点.
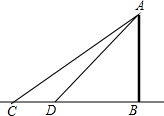 如图所示,对岸有一铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为40°,求铁塔AB的高.(结果保留整数)
如图所示,对岸有一铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为40°,求铁塔AB的高.(结果保留整数)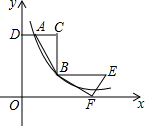 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.
如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.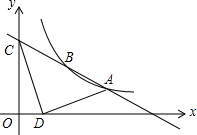 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(4,1)、B(2,2)两点,一次函数的图象与y轴的交点为C.
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(4,1)、B(2,2)两点,一次函数的图象与y轴的交点为C.