题目内容
18.解下列不等式,并把解集在数轴上表示出来:(1)2x+1>3;
(2)2-x<1;
(3)2(x+1)<3x;
(4)3(x+2)≥4(x-1)+7.
分析 (1)首先解不等式,进而在数轴上表示出解集;
(2)首先解不等式,进而在数轴上表示出解集;
(3)首先解不等式,进而在数轴上表示出解集;
(4)首先解不等式,进而在数轴上表示出解集.
解答 解:(1)2x+1>3,
解得:x>1,
如图所示: ;
;
(2)2-x<1,
解得:x>1,
如图所示: ;
;
(3)2(x+1)<3x,
解得:x>2,
如图所示: ;
;
(4)3(x+2)≥4(x-1)+7
解得:x≤3,
如图所示: .
.
点评 此题主要考查了解不等式以及在数轴上表示不等式的解集,正确解不等式是解题关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
3.某超市计划购进甲、乙两种品牌的新型节能台灯20盏,这两种台灯的进价和售价如下表所示:
设购进甲种台灯x盏,且所购进的两种台灯都能全部卖出.
(1)若该超市购进这批台灯共用去1000元,问这两种台灯购进多少盏?
(2)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(3)最终超市按照(2)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当毎盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
| 甲 | 乙 | |
| 进价(元/件) | 40 | 60 |
| 售价(元/件) | 60 | 100 |
(1)若该超市购进这批台灯共用去1000元,问这两种台灯购进多少盏?
(2)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(3)最终超市按照(2)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当毎盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
8.将左图案剪成若干小块,再分别平移后能够得到①、②、③中的( )


| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
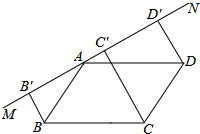 已知:如图,直线MN经过?ABCD的顶点A,BB′⊥MN,CC′⊥MN,DD′⊥MN,B′、C′、D′是垂足.
已知:如图,直线MN经过?ABCD的顶点A,BB′⊥MN,CC′⊥MN,DD′⊥MN,B′、C′、D′是垂足.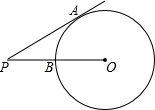 如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.
如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.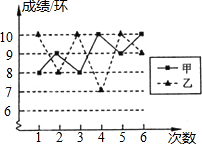 射击队为甲、乙两名运动员中选拨一人参加比赛,对他们进行了六次测试,测试成绩如图.
射击队为甲、乙两名运动员中选拨一人参加比赛,对他们进行了六次测试,测试成绩如图.