题目内容
15.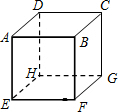 用大小相同、表面均为白色或红色的若干个小正方体拼接成如图所示的一个大正方体ABCD-EFGH.若大正方体的对角线AG、BH、CE、DF上所用的小正方体是表面均为红色的,而且共用了41个,大正方体其余部分用的都是表面均为白色的小正方体.则所用表面均为白色的小正方体共( )个.
用大小相同、表面均为白色或红色的若干个小正方体拼接成如图所示的一个大正方体ABCD-EFGH.若大正方体的对角线AG、BH、CE、DF上所用的小正方体是表面均为红色的,而且共用了41个,大正方体其余部分用的都是表面均为白色的小正方体.则所用表面均为白色的小正方体共( )个.| A. | 688 | B. | 959 | C. | 1290 | D. | 1687 |
分析 根据四条对角线一共41个,也就是每条对角线都有11个小正方体(共用一个中心),所以大正方体的边长为小正方体的11倍,故一共需要11×11×11=1331个小正方体,再减去所需红色正方体,即得.
解答 解:四条对角线一共41个,也就是每条对角线都有11个小正方体(共用一个中心),
所以大正方体的边长为小正方体的11倍,
故一共需要11×11×11=1331(个)小正方体,
1331-41=1290(个).
故选C.
点评 本题考查了认识立体图形,解决本题的关键是结合立体图形的特点解答.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
 在实数范围内有意义.
在实数范围内有意义.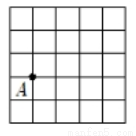
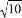 ,且点B在格点上.
,且点B在格点上.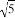 ,
,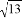 . 画一个△ABC
. 画一个△ABC ,使点C在格点上(只需画出符合条件的一个三角形).
,使点C在格点上(只需画出符合条件的一个三角形).