题目内容
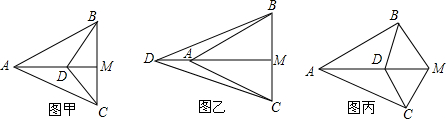
17．如图甲，已知AB=AC，M是BC的中点，点D是线段AM上的动点．（1）求证：BD=CD；
（2）如图乙，若点D在线段MA的延长线上，BD与CD还相等吗？为什么？
（3）如图丙，若M不是BC的中点，且BM=CM，则（1）中的结论还成立吗？为什么？
分析 （1）（2）根据等腰三角形的性质得到AM是BC的垂直平分线，得到答案；
（3）根据线段垂直平分线的判定得到AM是BC的垂直平分线，得到答案．
解答 证明：（1）∵AB=AC，M是BC的中点，
∴AM⊥BC，
∴AM是BC的垂直平分线，
∴BD=CD；
（2）BD=CD，
∵AB=AC，M是BC的中点，
∴AM⊥BC，
∴AM是BC的垂直平分线，
∴BD=CD；
（3）∵AB=AC，BM=CM，
∴AM是BC的垂直平分线，
∴BD=CD；
点评 本题考查的是线段垂直平分线的性质和判定、等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等、到线段的两个端点的距离相等的点在线段的垂直平分线上是解题的关键．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
在下列四个条件中：①AB=DC；②∠BAE=∠CDE；③BD=AC；④∠B=∠C．请
已知如图：CD、CE分别是AB边上的高、中线，且∠1=∠2=∠3．求证：∠ACB=90°．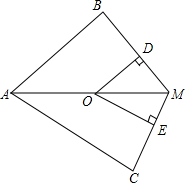
如图，已知AM平分∠BAC，点O是M上一点，OD⊥BM于点D，OE⊥CM于点E
如图，面积为96cm2的矩形被分成9个全等的矩形，求原矩形的长和宽（保留一位小数）．
6．方程3x（x-1）=5（x-1）的根为（ ）
| A． | x=$\frac{5}{3}$ | B． | x=1 | C． | x1=1，x2=$\frac{5}{3}$ | D． | x1=1，x2=$\frac{3}{5}$ |