题目内容
12. 已知如图:CD、CE分别是AB边上的高、中线,且∠1=∠2=∠3.求证:∠ACB=90°.
已知如图:CD、CE分别是AB边上的高、中线,且∠1=∠2=∠3.求证:∠ACB=90°.
分析 过E作EF⊥BC于F,由∠1=∠2,且CD⊥AB,于是得到AD=DE,AC=CE,∠CEA=∠A,根据∠2=∠3,且DE⊥CD,EF⊥BC,推出∠CEF=∠CED,EF=DE=AD=$\frac{1}{2}$AE=$\frac{1}{2}$BE,且EF⊥BC,求得∠B=30°,∠BEF=60°,即可得到结论.
解答 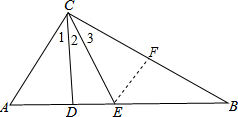 证明:过E作EF⊥BC于F,
证明:过E作EF⊥BC于F,
∵∠1=∠2,且CD⊥AB,
∴AD=DE,AC=CE,∠CEA=∠A,
∵∠2=∠3,且DE⊥CD,EF⊥BC,
∴∠CEF=∠CED,EF=DE=AD=$\frac{1}{2}$AE=$\frac{1}{2}$BE,且EF⊥BC,
∴∠B=30°,∠BEF=60°,
∴∠A=∠CED=∠CEF=$\frac{1}{2}$(180°-∠BEF)=$\frac{1}{2}$(180°-60°)=60°,
∴∠ACB=180°-∠A-∠B=180°-60°-30°=90°.
点评 本题考查了三角形的内角和,等腰三角形的性质,直角三角形的判定,正确的作出辅助线是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4.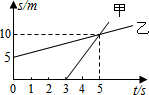 甲、乙两物体沿同一条直线向东运动,其运动的路程S随时间t变化的图象如图所示,以下说法中正确的是( )
甲、乙两物体沿同一条直线向东运动,其运动的路程S随时间t变化的图象如图所示,以下说法中正确的是( )
 甲、乙两物体沿同一条直线向东运动,其运动的路程S随时间t变化的图象如图所示,以下说法中正确的是( )
甲、乙两物体沿同一条直线向东运动,其运动的路程S随时间t变化的图象如图所示,以下说法中正确的是( )| A. | 甲物体比乙物体早运动3s | |
| B. | 甲物体比乙物体运动得慢 | |
| C. | 从第3s开始,v甲>v乙,5s末甲、乙相遇 | |
| D. | 5s内甲、乙两物体的平均速度相等 |
 如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.
如图所示,DE∥BC,∠1=∠2,求证:EF∥AB. 如图,在△ABC中,AB=AC,DE是腰AB上的中垂线,若∠A=30°,求∠EBC的大小.
如图,在△ABC中,AB=AC,DE是腰AB上的中垂线,若∠A=30°,求∠EBC的大小.