题目内容
11．阅读下面的解答过程，求y2+4y+8的最小值．解：y2+4y+8=y2+4y+4+4=（y+2）2+4≥4，
∵（y+2）2≥0即（y+2）2的最小值为0，
∴y2+4y+8的最小值为4．
仿照上面的解答过程，求x2-12x+41的最小值．
分析 多项式配方后，根据完全平方式恒大于等于0，即可求出最小值．
解答 解：x2-12x+41
=x2-12x+36+5
=（x-6）2+5≥5，
∵（x-6）2≥0即（x-6）2的最小值为0，
∴x2-12x+41的最小值为5．
点评 此题考查了配方法的应用，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
1．已知一次函数y=kx+b的图象经过第一、二、四象限，则函数y=$\frac{kb}{x}$的图象在（ ）
| A． | 第一、三象限 | B． | 第二、四象限 | C． | 第三、四象限 | D． | 第一、二象限 |
学校要围一个矩形花圃，其一边利用足够长的墙，另三边用篱笆围成，由于园艺需要，还要用一段篱笆将花圃分隔为两个小矩形部分（如图所示），总共36米的篱笆恰好用完（不考虑损耗）．设矩形垂直于墙面的一边AB的长为x米（要求AB＜AD），矩形花圃ABCD的面积为S平方米．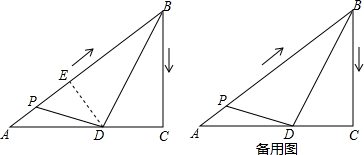
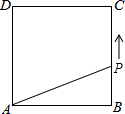如图，在边长为$\sqrt{2}$的正方形ABCD的一边BC上，有一点P从B点运动到C点，设PB=x，四边形APCD的面积为y．写出y与x之间的关系式为y=-$\frac{\sqrt{2}}{2}$x+2（0≤x＜$\sqrt{2}$）（要写出自变量的取值范围）．
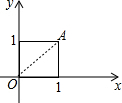如图，在平面直角坐标系中，点A的坐标是（1，1），如果将线段OA绕点O旋转135°，得线段OB，求点B的坐标？