题目内容
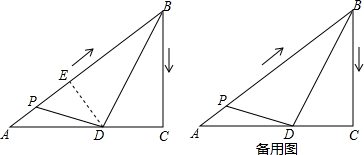
6.如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P以1cm/s的速度从A开始沿着折线AB-BC运动到点C,点D在AC上,连接BD,PD,设点P的运动时间为t秒;(1)直接写出AB的长度;
(2)把△BCD沿着BD对折,点C恰好落在AB上的点E处,求此时CD的长;
(3)若点D在(2)中的位置,当t为几秒时,△BPD为直角三角形?
分析 (1)直接根据勾股定理求出AB的长即可;
(2)根据点C恰好落在AB上的点E处可得出△BCD≌△BED,故BC=BE,由此可得出AE的长,利用勾股定理求出DE的长即可;
(3)分∠BDP=90°与∠BED=90°两种情况进行分类讨论即可.
解答 解:(1)∵在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10cm;
(2)∵点C恰好落在AB上的点E处,
∴△BCD≌△BED,
∴BC=BE=6cm,CD=DE=x,
∴AE=10-6=4cm.
设CD=DE=x,则AD=8-x,
在Rt△ADE中,
∵AE2+DE2=AD2,即42+x2=(8-x)2,解得x=3cm.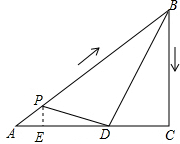
答:此时CD的长为3cm;
(3)当∠BDP=90°时,
∵CD=3cm,BC=6cm,
∴BD2=32+62=45cm;
过点P作PE⊥AC于点E,设AP=t,则BP=10-t,
∵PE⊥AC,
∴$\frac{AE}{AC}$=$\frac{AP}{AB}$=$\frac{PE}{BC}$,即$\frac{AE}{8}$=$\frac{t}{10}$=$\frac{PE}{6}$,解得AE=$\frac{4}{5}$t,PE=$\frac{3}{5}$t,
∴PD=$\sqrt{{PE}^{2}+{DE}^{2}}$=$\sqrt{{(\frac{3}{5}t)}^{2}+{(\frac{4}{5}t)}^{2}}$=t.
∵BD2+PD2=BP2,即45+t2=(10-t)2,解得t=2.75(秒);
当∠BPD=90°且点P在AB上时,由(1)可知,此时BP=BC=6cm,
∴AP=10-6=4cm,
∴t=4(秒);
当∠BPD=90°且点P在BC上时,点P与点C重合,故t=AB+BC=10+6=16(秒).
综上所述,当t=2.75秒或4秒或16秒时,△BPD为直角三角形.
点评 本题考查的是几何变换综合题,涉及到直角三角形的性质、图形翻折变换的性质及相似三角形的判定与性质,在解答此题时要注意进行分类讨论.

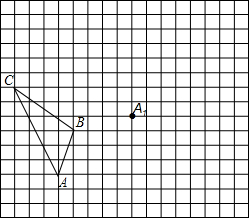 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.画出△ABC关于点A1的中心对称图形.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.画出△ABC关于点A1的中心对称图形. 如图:在四边形ABCD中,BC>DA,AD=DC,BD平分∠ABC,DH⊥BC于H,求证:
如图:在四边形ABCD中,BC>DA,AD=DC,BD平分∠ABC,DH⊥BC于H,求证: 如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE=4$\sqrt{3}$.
如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE=4$\sqrt{3}$.