题目内容
16．
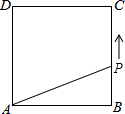如图，在边长为$\sqrt{2}$的正方形ABCD的一边BC上，有一点P从B点运动到C点，设PB=x，四边形APCD的面积为y．写出y与x之间的关系式为y=-$\frac{\sqrt{2}}{2}$x+2（0≤x＜$\sqrt{2}$）（要写出自变量的取值范围）．
分析 根据正方形的性质和梯形面积公式即可求出y与x的函数关系式，容易确定自变量的取值范围．
解答 解：∵PB=x，正方形边长为$\sqrt{2}$，
∴梯形APCD的面积y=$\frac{1}{2}$×（$\sqrt{2}$+$\sqrt{2}$-x）×$\sqrt{2}$=-$\frac{\sqrt{2}}{2}$x+2，
∴y与x的函数关系式为：y=-$\frac{\sqrt{2}}{2}$x+2（0≤x＜$\sqrt{2}$）．
故答案为：y=-$\frac{\sqrt{2}}{2}$x+2（0≤x＜$\sqrt{2}$）．
点评 本题考查了函数关系式的确定、正方形的性质、梯形面积的计算，属于基础题，关键是根据梯形面积公式求出y与x的函数关系式．
练习册系列答案
相关题目
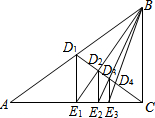如图，已知Rt△ABC，D1是斜边AB的中点，过D1作D1E1⊥AC于E1，连结BE1交CD1于D2；过D2作D2E2⊥AC于E2，连结BE2交CD1于D3；过D3作D3E3⊥AC于E3，…，如此继续，可以依次得到点D4，D5，…，Dn，分别记△BD1E1，△BD2E2，△BD3E3，…，△BDnEn的面积为S1，S2，S3，…Sn．若S△ABC=1，则S2010=$\frac{1}{201{1}^{2}}$．