题目内容
1．
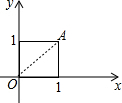如图，在平面直角坐标系中，点A的坐标是（1，1），如果将线段OA绕点O旋转135°，得线段OB，求点B的坐标？
分析 由A的坐标和勾股定理求出OA，利用旋转性质求出点A旋转后的对应点的坐标即可；注意分两种情况讨论．
解答 解：∵A（1，1），
由勾股定理得：OA=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，
分两种情况：
①线段OA绕点O按逆时针方向旋转135°，则点B在x轴负半轴上，
∴B（-$\sqrt{2}$，0）；
②线段OA绕点O按顺时针方向旋转135°，则点B在y轴负半轴上，
∴B（0，-$\sqrt{2}$）；
综上所述：点B的坐标为（-$\sqrt{2}$，0）或（0，-$\sqrt{2}$）．
点评 此题考查了坐标与图形变化-旋转、勾股定理，熟练掌握旋转的性质是解本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目