题目内容
20.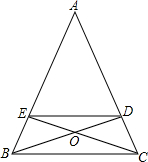 已知,如图,△ABC中,AB=AC,BD,CE为△ABC的高,且BD,CE交于点O.
已知,如图,△ABC中,AB=AC,BD,CE为△ABC的高,且BD,CE交于点O.(1)图中共有几个等腰三角形?分别是哪些三角形?
(2)其中△ODE是等腰三角形吗?若是,请说明理由;
(3)若∠A=45°,还有哪些三角形也是等腰三角形?OE与DC会相等吗?请说明理由.
分析 (1)根据等腰三角形的判定定理判断即可;
(2)由AB=AC,得到∠ABC=∠ACB,由于BD,CE为△ABC的高,于是得到∠BEC=∠CDB=90°,证得BO=CO,推出△EBC≌△DCB,证得BD=EC,根据线段的和差即可得到结果;
(3)根据等腰直角三角形的判定定理就可得到△ABD,△ACE,△BEO,△DCO也是等腰三角形,由于∠A=45°,BD,CE为△ABC的高,得到△BEO,△DCO是等腰三角形,即可得到结论.
解答 解:(1)图中有四个等腰三角形,分别是△ABC,△BOC,△AED,△OED;
(2)△OED是等腰三角形,理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵BD,CE为△ABC的高,
∴∠BEC=∠CDB=90°,
∴∠ECB=∠DBC,
∴BO=CO,
在△EBC与△DCB中,
$\left\{\begin{array}{l}{∠ABC=∠ACB}\\{∠BEC=∠CDB}\\{BC=BC}\end{array}\right.$,
∴△EBC≌△DCB,
∴BD=EC,
∴OD=BD-OB,OE=CE-OC,
∴OE=OD,
∴△OED是等腰三角形;
(3)若∠A=45°,△ABD,△ACE,△BEO,△DCO也是等腰三角形,OE=DC,理由如下:
∵∠A=45°,BD,CE为△ABC的高,
∴∠ABD=∠ACE=45°,
∴∠BOE=∠DOC=45°,
∴BE=OE,OD=CD,
∵OE=OD,
∴OE=CD.
点评 本题考查了等腰三角形的判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,熟练掌握等腰三角形的判定和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,某小区内有一块长、宽比为2:1的矩形空地,计划在该空地上修筑两条宽为2m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312m2,请求出原来大矩形空地的长和宽.
如图,某小区内有一块长、宽比为2:1的矩形空地,计划在该空地上修筑两条宽为2m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312m2,请求出原来大矩形空地的长和宽.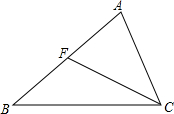 如图,F是△ABC的AB边上一点,下列结论正确的个数是( )
如图,F是△ABC的AB边上一点,下列结论正确的个数是( )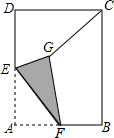 如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.
如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.