��Ŀ����
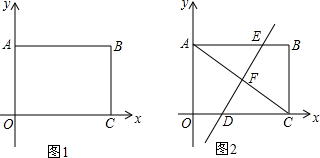
5������ABCD�У������Խ���AC��BD�ཻ�ڵ�O����MON+��BCD=180�㣬��MON�Ƶ�O��ת������OM����BC�ڵ�E������ON����DC�ڵ�F������EF����1����ͼ1������ABC=90��ʱ����OEF����״�ǵ���ֱ�������Σ�
��2����ͼ2������ABC=60��ʱ�����жϡ�OEF����״����˵�����ɣ�
��3���ڣ�1���������£�����MON�Ķ����Ƶ�AO���е�O�䴦����MO��N�Ƶ�O����ת���������MO��N+��BCD=180�㣬����O��M��ֱ��BC�ڵ�E������O��N��ֱ��CD�ڵ�F����BC=4����$\frac{{S}_{��O��EF}}{{S}_{�ı���ABCD}}$=$\frac{9}{8}$ʱ��ֱ��д���߶�CE�ij���
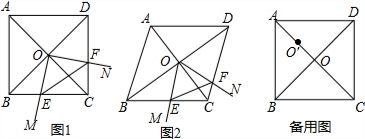
���� ��1��������ı���ABCD�������Σ�Ȼ����������ε����ʿɵá�EBO=��FCO=45�㣬OB=OC���ٸ���ͬ�ǵ������ȿɵá�BOE=��COF��Ȼ�����á��DZ߽ǡ�֤����BOE�͡�COFȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤��
��2����O����OG��BC��G����OH��CD��H���������ε����ʿɵ�CAƽ�֡�BCD����ABC+��BCD=180�㣬���OG=OH����BCD=180��-60��=120�㣬�Ӷ���á�GOH=��EOF=60�㣬�ٸ��ݵ����������ɵá�EOG=��FOH��Ȼ�����á��DZ߽ǡ�֤����EOG�͡�FOHȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤��
��3����O����OG��BC��G����OH��CD��H��������ı���O��GCH�������Σ��Ӷ����GC=O��G=3����GO��H=90�㣬Ȼ�����á��DZ߽ǡ�֤����EO��G�͡�FO��Hȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ���֤�á�O��EF�ǵ���ֱ�������Σ�������֪��õ���ֱ�������ε�ֱ�DZ�O��E�ij���Ȼ����ݹ��ɶ������EG���������CE�ij���
���  ��1����OEF�ǵ���ֱ�������Σ�
��1����OEF�ǵ���ֱ�������Σ�
֤������ͼ1��������ABCD�У���ABC=90�㣬
���ı���ABCD�������Σ�
��OB=OC����BOC=90�㣬��BCD=90�㣬��EBO=��FCO=45�㣬
���BOE+��COE=90�㣬
�ߡ�MON+��BCD=180�㣬
���MON=90�㣬
���COF+��COE=90�㣬
���BOE=��COF��
�ڡ�BOE���COF�У�
$\left\{\begin{array}{l}{��BOE=��COF}\\{OB=OC}\\{��EBO=��FCO}\end{array}\right.$��
���BOE�ա�COF��ASA����
��OE=OF��
���OEF�ǵ���ֱ�������Σ�
�ʴ�Ϊ����ֱ�������Σ�
��2����OEF�ǵȱ������Σ�
֤������ͼ2����O����OG��BC��G����OH��CD��H��
���OGE=��OGC=��OHC=90�㣬
���ı���ABCD�����Σ�
��CAƽ�֡�BCD����ABC+BCD=180�㣬
��OG=OH����BCD=180��-60��=120�㣬
�ߡ�GOH+��OGC+��BCD+��OHC=360�㣬
���GOH+��BCD=180�㣬
���MON+��BCD=180�㣬
���GOH=��EOF=60�㣬
�ߡ�GOH=��GOF+��FOH����EOF=��GOF+��EOG��
���EOG=��FOH��
�ڡ�EOG���FOH�У�
$\left\{\begin{array}{l}{��EOG=��FOH}\\{OG=OH}\\{��EGO=��FHO}\end{array}\right.$��
���EOG�ա�FOH��ASA����
��OE=OF��
���OEF�ǵȱ������Σ�
��3��֤������ͼ3��������ABCD�У���ABC=90�㣬
���ı���ABCD�������Σ�
��$\frac{O��C}{AC}$=$\frac{3}{4}$��
��O����O��G��BC��G����O��H��CD��H��
���O��GC=��O��HC=��BCD=90�㣬
���ı���O��GCH�Ǿ��Σ�
��O��G��AB��O��H��AD��
��$\frac{O��G}{AB}$=$\frac{O��H}{AD}$=$\frac{O��C}{AC}$=$\frac{3}{4}$��
��AB=BC=CD=AD=4��
��O��G=O��H=3��
���ı���O��GCH�������Σ�
��GC=O��G=3����GO��H=90��
�ߡ�MO��N+��BCD=180�㣬
���EO��F=90�㣬
���EO��F=��GO��H=90�㣬
�ߡ�GO��H=��GO��F+��FO��H����EO��F=��GO��F+��EO��G��
���EO��G=��FO��H��
�ڡ�EO��G���FO��H�У�
$\left\{\begin{array}{l}{��EO��G=��FO��H}\\{O��G=O��H}\\{��EGO��=��FHO��}\end{array}\right.$��
���EO��G�ա�FO��H��ASA����
��O��E=O��F��
���O��EF�ǵ���ֱ�������Σ�
��S������ABCD=4��4=16��$\frac{{S}_{��O��EF}}{{S}_{�ı���ABCD}}$=$\frac{9}{8}$��
��S��O��EF=18��
��S��O��EF=$\frac{1}{2}$O��E2��
��O��E=6��
��RT��O��EG��EG=$\sqrt{O��{E}^{2}-O{��G}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$��
��CE=CG+EG=3+3$\sqrt{3}$��
���ݶԳ��Կ�֪������M��ON����ת����ͼ��ʾλ��ʱ��
CE��=E��G-CG=3$\sqrt{3}$-3��
���Ͽɵã��߶�CE�ij�Ϊ3+3$\sqrt{3}$��3$\sqrt{3}$-3��
���� ���⿼���������ε����ʣ����ε����ʣ�������ȫ�ȵ��ж������ʣ������������Ĺؼ�����ȷ��������ת����������ȷ�����������ǹؼ���

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�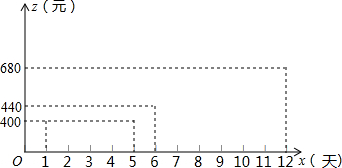 �ڡ�������óǢ̸�ᡱ�ϣ�����ij��װ���ӵ�����һ�����ڷ�װ�Ķ�����Ҫ�������12�죨��12�죩�ڱ��ʱ�����ɣ��ҵ���ӹ��ķ�װ�������������ߣ�Ϊ�˼ӿ���ȣ������ȡ����������Ϣ��������������ת��������ʽ������Ч�ʵõ�����ߣ�����ÿ�������ķ�װ����y���ף���ʱ��x��Ԫ���Ĺ�ϵ�����
�ڡ�������óǢ̸�ᡱ�ϣ�����ij��װ���ӵ�����һ�����ڷ�װ�Ķ�����Ҫ�������12�죨��12�죩�ڱ��ʱ�����ɣ��ҵ���ӹ��ķ�װ�������������ߣ�Ϊ�˼ӿ���ȣ������ȡ����������Ϣ��������������ת��������ʽ������Ч�ʵõ�����ߣ�����ÿ�������ķ�װ����y���ף���ʱ��x��Ԫ���Ĺ�ϵ�����| ʱ��x���죩 | 1 | 2 | 3 | 4 | �� |
| ÿ�����y���ף� | 22 | 24 | 26 | 28 | �� |
��1���ж�ÿ�������ķ�װ������y���ף�������ʱ��x��Ԫ��֮��������ѧ�������ֺ�����ϵ������֤��
��2����֪������ó��װ�Ķ����۸�Ϊÿ��1570Ԫ���賵��ÿ�������Ϊw��Ԫ������w��Ԫ����x���죩֮��ĺ�����ϵʽ���������һ����������������������������Ƕ���Ԫ��
��3���ӵ�6���𣬸ó������ó���ÿ����һ��װ�;�aԪ��ɽ�������ض�ͯ��Ϊ��ͼ���ҵĻ��𣬵����뱣֤ÿ��۳������������ʱ��������������a�����ֵ����ʱ���ض�ͯ���ö���Ԫ����
| A�� | 1 | B�� | -$\frac{2}{3}$ | C�� | -1 | D�� | $\frac{2}{3}$ |