题目内容
1．已知a，b为整数，且满足a（$\sqrt{2}$+1）+3（b-2$\sqrt{2}$）=6+3$\sqrt{2}$，求a+b的值．分析 已知等式整理后，利用相等的条件列出方程组，求出方程组的解得到a与b的值，即可求出a+b的值．
解答 解：已知等式整理得：（a-6）$\sqrt{2}$+a+3b=3$\sqrt{2}$+6，
可得$\left\{\begin{array}{l}{a-6=3}\\{a+3b=6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=9}\\{b=-1}\end{array}\right.$，
则a+b=9-1=8．
点评 此题考查了实数的运算，以及解二元一次方程组，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，已知直线AB、CD、EF交于O点，∠AOE=45°，∠DOF=30°，求∠BOC的度数．
如图，在Rt△ABC中，∠C=90°，AB=10，点D是直角边AC上一点，且满足cos∠ABD=$\frac{4}{5}$，∠A=∠CBD，求线段BD的长度．
9．下列各式计算正确的是（ ）
| A． | $2\sqrt{-8}=-2$ | B． | ${（{-\sqrt{2}}）^2}=4$ | C． | $\sqrt{{{（{-3}）}^2}}=-3$ | D． | $\sqrt{16}$=4 |
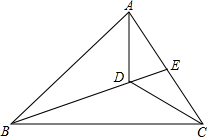三角形不等式是指一个三角形的两边长度之和大于第三边的长度．在图中，E位于线段AC上，D位于线段BE上．