题目内容
12.已知关于x的一元二次方程为2x2-x+m(4x-1)-3=0.(1)m为何值时,方程的一根为-1;
(2)m为何值时,两根异号,且正根的绝对值较大.
分析 (1)将x=-1代入,解关于m的方程即可;
(2)由题意知两根之和大于0、两根之积小于0,据此列不等式组求解可得.
解答 解:(1)将x=-1代入方程,得:2+1-5m-3=0,
解得:m=0,
即m=0时,方程的一根为-1;
(2)方程整理,得:2x2+(4m-1)x-m-3=0,
根据题意,得:$\left\{\begin{array}{l}{-\frac{4m-1}{2}>0}\\{\frac{-m-3}{2}<0}\end{array}\right.$,
解得:-3<m<$\frac{1}{4}$.
点评 本题主要考查根与系数的关系,熟练掌握方程的解和韦达定理是解题的关键.

练习册系列答案
相关题目
5.下列方程变形中,正确的是( )
| A. | 方程3x-2=2x+1,移项得,3x-2x=-1+2 | |
| B. | 方程3-x=2-5( x-1),去括号得,3-x=2-5x-1 | |
| C. | 方程$\frac{2}{3}t=\frac{3}{2}$,系数化为1得,t=1 | |
| D. | 方程$\frac{x-1}{0.2}-\frac{x}{0.5}=1$,去分母得,5( x-1)-2x=1 |
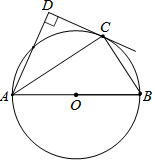 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.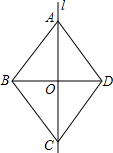 如图,直线l是四边形ABCD的对称轴,如果AD∥BC,求证:AO=OC.
如图,直线l是四边形ABCD的对称轴,如果AD∥BC,求证:AO=OC.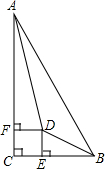 已知:如图,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E、F.求证:四边形CEDF是正方形.
已知:如图,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E、F.求证:四边形CEDF是正方形.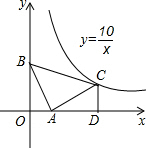 如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).
如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).