题目内容
9.下列各式计算正确的是( )| A. | $2\sqrt{-8}=-2$ | B. | ${({-\sqrt{2}})^2}=4$ | C. | $\sqrt{{{({-3})}^2}}=-3$ | D. | $\sqrt{16}$=4 |
分析 直接利用二次根式的性质分别化简判断即可.
解答 解:A、2$\sqrt{-8}$,无意义,故此选项不合题意;
B、(-$\sqrt{2}$)2=2,故此选项不合题意;
C、$\sqrt{(-3)^{2}}$=3,故此选项不合题意;
D、$\sqrt{16}$=4,正确,符合题意.
故选:D.
点评 此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
18. 如图,图中对顶角共有( )对.
如图,图中对顶角共有( )对.
 如图,图中对顶角共有( )对.
如图,图中对顶角共有( )对.| A. | 3 | B. | 6 | C. | 8 | D. | 12 |
13.已知三角形两边长分别是a,b(b>a),则三角形的周长C应满足( )
| A. | 2b<C<2(a+b) | B. | a+b<C<3b | C. | 2a+b<C<a+2b | D. | 2(a+b)<C<a+3b |
17.为了加强公民的节约意识,我市出台阶梯电价计算方案如下表:
(1)某户居民2月份应缴电费78元,该户居民2月份用电多少度?
(2)某户居民10月份用电220度,应缴电费111元,求a的值;
(3)用x(度)表示月用电量,请根据x的不同取值范围用含x的代数式表示该月应缴电费.
| 价目表 | |
| 不超过200度的部分 | 0.50元/度 |
| 超过200度不超过400度的部分 | a元/度 |
| 超过400度的部分 | 0.80元/度 |
| 注:电费按月结算 | |
(2)某户居民10月份用电220度,应缴电费111元,求a的值;
(3)用x(度)表示月用电量,请根据x的不同取值范围用含x的代数式表示该月应缴电费.
17.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:
(1)若一户居民七月份用电420度,则需缴电费多少元?
(2)若一户居民某月用电x度(x大于200小于400),则需缴电费多少元?(用含x的代数式表示)
(3)某户居民五、六月份共用电500度,缴电费262元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?
| 档次 | 每户每月用电数(度) | 执行电价(元/度) |
| 第一档 | 小于200部分 | 0.5 |
| 第二档 | 200小于等于400部分 | 0.6 |
| 第三档 | 大于400部分 | 0.8 |
(2)若一户居民某月用电x度(x大于200小于400),则需缴电费多少元?(用含x的代数式表示)
(3)某户居民五、六月份共用电500度,缴电费262元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?
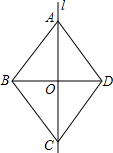 如图,直线l是四边形ABCD的对称轴,如果AD∥BC,求证:AO=OC.
如图,直线l是四边形ABCD的对称轴,如果AD∥BC,求证:AO=OC.
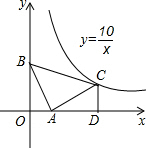 如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).
如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).