题目内容
(1)计算:|3-2
|+(π-2014)0+(
)-1
(2)化简:(1-
)÷(
-2)
(3)求不等式组
的解集.
| 3 |
| 1 |
| 2 |
(2)化简:(1-
| 1 |
| x2-2x+1 |
| x2-2 |
| x-1 |
(3)求不等式组
|
考点:分式的混合运算,实数的运算,零指数幂,负整数指数幂,解一元一次不等式组
专题:计算题
分析:(1)根据零指数幂和负整数指数幂的意义得到原式=2
-3+1+2,然后合并即可;
(2)先把括号的分式进行通分,再把分子分母因式分解和除法运算化为乘法运算,然后约分即可;
(3)分别接两个不等式得到x≤4和x>-
,然后根据大于小的小于大的取中间确定不等式组的解集.
| 3 |
(2)先把括号的分式进行通分,再把分子分母因式分解和除法运算化为乘法运算,然后约分即可;
(3)分别接两个不等式得到x≤4和x>-
| 3 |
| 2 |
解答:解:(1)原式=2
-3+1+2=2
;
(2)原式=
÷
=
•
=
;
(3)
,
解①得x≤4,
解②得x>-
,
所以不等式组的解集为-
<x≤4.
| 3 |
| 3 |
(2)原式=
| x2-2x+1-1 |
| (x-1)2 |
| x2-2-2(x-1) |
| x-1 |
=
| x(x-2) |
| (x-1)2 |
| x-1 |
| x(x-2) |
=
| 1 |
| x-1 |
(3)
|
解①得x≤4,
解②得x>-
| 3 |
| 2 |
所以不等式组的解集为-
| 3 |
| 2 |
点评:本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.也考查了实数的运算、零指数幂和负整数指数幂以及解一元一次不等式组.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
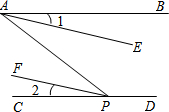 如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2,请填写AE∥PF的理由.
如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2,请填写AE∥PF的理由.