题目内容
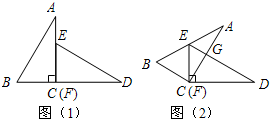 如图所示,已知△ACB△DFE与是两个全等的直角三角形,量得它们的斜边长为2cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B.C.F.D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则线段FG的长为( )
如图所示,已知△ACB△DFE与是两个全等的直角三角形,量得它们的斜边长为2cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B.C.F.D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则线段FG的长为( )A、2
| ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:旋转的性质
专题:
分析:由题意得在△ACB和△DFE中,∠ACB=∠DFE=90°,∠A=∠D=30°,AB=DE=2,则可计算出∠B=∠DEF=60°,BC=EF=1,再利用旋转的性质得到CB=CE=1,∠B=60°,则可判断△CBE为等边三角形,得到∠BCE=60°,于是可计算出∠ECG=30°,接着得到∠CGE=90°,然后根据含30度的直角三角形三边的关系可计算出FG的长.
解答:解:在△ACB和△DFE中,∠ACB=∠DFE=90°,∠A=∠D=30°,AB=DE=2,
则∠B=∠DEF=60°,BC=EF=1,
∵图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,
∴CB=CE=1,∠B=60°,
∴△CBE为等边三角形,
∴∠BCE=60°,
∴∠ECG=∠BCA-∠BCE=30°,
∵∠DEF=60°,
∴∠CGE=90°,
∴EG=
FE=
,
∴FG=
EG=
.
故选C.
则∠B=∠DEF=60°,BC=EF=1,
∵图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,
∴CB=CE=1,∠B=60°,
∴△CBE为等边三角形,
∴∠BCE=60°,
∴∠ECG=∠BCA-∠BCE=30°,
∵∠DEF=60°,
∴∠CGE=90°,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
∴FG=
| 3 |
| ||
| 2 |
故选C.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
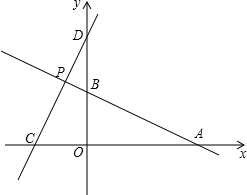 如图,直线AB:y=-
如图,直线AB:y=-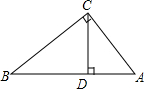 如图,已知Rt△ABC中,∠C=90°,CD⊥AB于D,利用三角函数知识证明:
如图,已知Rt△ABC中,∠C=90°,CD⊥AB于D,利用三角函数知识证明: 如图,篱笆(虚线部分)的长度是15cm,如何围篱笆才能使所围矩形的面积最大.
如图,篱笆(虚线部分)的长度是15cm,如何围篱笆才能使所围矩形的面积最大.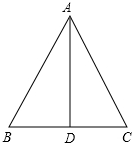 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,BD=2cm,求BC的长和∠ADC的大小.
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,BD=2cm,求BC的长和∠ADC的大小.