题目内容
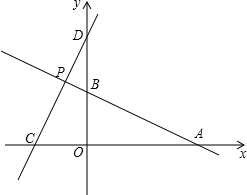 如图,直线AB:y=-
如图,直线AB:y=-| 1 |
| 2 |
(1)求四边形PCOB的面积;
(2)直线CD上是否存在点M,使得△PAM的面积等于四边形PCOB的面积?若存在,求出点M的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:综合题
分析:(1)过点P作PH⊥x轴于点H,如图1,由条件易求出点A、B、C、D、P的坐标,从而可求出OA、OB、OC、OD、OH、PH、CH的值,然后运用割补法就可求出四边形PCOB的面积.
(2)①若点M在点P的上方,过点M作ME⊥x轴于点E,如图2,可先求出△PCA的面积,从而得到△MCA的面积,进而得到ME的长(即点M的纵坐标),由点M在直线CD上可求出点M的横坐标,就可得到点M的坐标;②若点M在点P的下方,过点M作ME⊥x轴于点E,如图3,仿照①中的解题过程,就可求出点M的坐标.
(2)①若点M在点P的上方,过点M作ME⊥x轴于点E,如图2,可先求出△PCA的面积,从而得到△MCA的面积,进而得到ME的长(即点M的纵坐标),由点M在直线CD上可求出点M的横坐标,就可得到点M的坐标;②若点M在点P的下方,过点M作ME⊥x轴于点E,如图3,仿照①中的解题过程,就可求出点M的坐标.
解答:解:(1)过点P作PH⊥x轴于点H,如图1.
∵直线y=-
x+2与x轴、y轴分别交于A、B两点,
∴点A的坐标为(4,0),点B的坐标为(0,2),
∴OA=4,OB=2.
∵直线y=2x+4与x轴、y轴分别交于C、D两点,
∴点C的坐标为(-2,0),点D的坐标为(0,4),
∴OC=2,OD=4.
联立
,
解得:
.
∵点P是直线y=-
x+2与直线y=2x+4的交点,
∴点P的坐标为(-
,
),
∴OH=
,PH=
,
∴CH=CO-OH=2-
=
,
∴S四边形PCOB=S△CHP+S梯形PHOB
=
×
×
+
×(
+2)×
=
,
∴四边形PCOB的面积为
.
(2)直线CD上存在点M,使得△PAM的面积等于四边形PCOB的面积.
①若点M在点P的上方,过点M作ME⊥x轴于点E,如图2.
由题可得:S△MPA=S四边形PCOB=
.
∵S△PCA=
AC•PH=
×6×
=
,
∴S△MCA=S△PCA+S△MPA=
+
=
,
∴
×6×ME=
,
∴ME=
,即yM=
.
∵点M在直线y=2x+4上,
∴2xM+4=
,
∴xM=-
,
∴点M的坐标为(-
,
).
②若点M在点P的下方,过点M作ME⊥x轴于点E,如图3.
∵S△MPA=S四边形PCOB=
,S△PCA=
AC•PH=
×6×
=
,
∴S△MCA=S△PCA-S△MPA=
-
=4,
∴
×6×ME=4,
∴ME=
,即yM=
.
∵点M在直线y=2x+4上,
∴2xM+4=
,
∴xM=-
,
∴点M的坐标为(-
,
).
综上所述:符合条件的点M的坐标为(-
,
)或(-
,
).
∵直线y=-
| 1 |
| 2 |
∴点A的坐标为(4,0),点B的坐标为(0,2),
∴OA=4,OB=2.
∵直线y=2x+4与x轴、y轴分别交于C、D两点,
∴点C的坐标为(-2,0),点D的坐标为(0,4),
∴OC=2,OD=4.

联立
|
解得:
|
∵点P是直线y=-
| 1 |
| 2 |
∴点P的坐标为(-
| 4 |
| 5 |
| 12 |
| 5 |
∴OH=
| 4 |
| 5 |
| 12 |
| 5 |
∴CH=CO-OH=2-
| 4 |
| 5 |
| 6 |
| 5 |
∴S四边形PCOB=S△CHP+S梯形PHOB
=
| 1 |
| 2 |
| 6 |
| 5 |
| 12 |
| 5 |
| 1 |
| 2 |
| 12 |
| 5 |
| 4 |
| 5 |
| 16 |
| 5 |
∴四边形PCOB的面积为
| 16 |
| 5 |
(2)直线CD上存在点M,使得△PAM的面积等于四边形PCOB的面积.
①若点M在点P的上方,过点M作ME⊥x轴于点E,如图2.

由题可得:S△MPA=S四边形PCOB=
| 16 |
| 5 |
∵S△PCA=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
| 36 |
| 5 |
∴S△MCA=S△PCA+S△MPA=
| 36 |
| 5 |
| 16 |
| 5 |
| 52 |
| 5 |
∴
| 1 |
| 2 |
| 52 |
| 5 |
∴ME=
| 52 |
| 15 |
| 52 |
| 15 |
∵点M在直线y=2x+4上,
∴2xM+4=
| 52 |
| 15 |
∴xM=-
| 4 |
| 15 |
∴点M的坐标为(-
| 4 |
| 15 |
| 52 |
| 15 |
②若点M在点P的下方,过点M作ME⊥x轴于点E,如图3.

∵S△MPA=S四边形PCOB=
| 16 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
| 36 |
| 5 |
∴S△MCA=S△PCA-S△MPA=
| 36 |
| 5 |
| 16 |
| 5 |
∴
| 1 |
| 2 |
∴ME=
| 4 |
| 3 |
| 4 |
| 3 |
∵点M在直线y=2x+4上,
∴2xM+4=
| 4 |
| 3 |
∴xM=-
| 4 |
| 3 |
∴点M的坐标为(-
| 4 |
| 3 |
| 4 |
| 3 |
综上所述:符合条件的点M的坐标为(-
| 4 |
| 15 |
| 52 |
| 15 |
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题考查了直线与坐标轴的交点问题、直线与直线的交点问题,运用割补法是解决第(1)小题的关键,运用分类讨论的数学思想是解决第(2)小题的关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
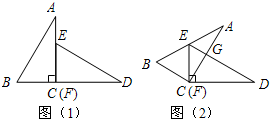 如图所示,已知△ACB△DFE与是两个全等的直角三角形,量得它们的斜边长为2cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B.C.F.D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则线段FG的长为( )
如图所示,已知△ACB△DFE与是两个全等的直角三角形,量得它们的斜边长为2cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B.C.F.D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则线段FG的长为( )