题目内容
A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A,B两校运往甲、乙两校的费用如下表:
(1)设A校运往C校的电脑为x台,求总运费y(元)关于x的函数关系式,直接写出x的取值范围;
(2)求出总运费最低的调运方案,最低运费是多少?
| C校(元/台) | D校(元/台) | |
| A校 | 40 | 80 |
| B校 | 0 | 50 |
(2)求出总运费最低的调运方案,最低运费是多少?
考点:一次函数的应用
专题:
分析:(1)表示出从A校运往D校,从B校运往C校和D校的电脑台数,然后根据列出费用表达式整理即可,再根据运往各校的电脑台数不小于0列式求解即可得到x的取值范围;
(2)根据一次函数的增减性求出x的值,然后解答即可.
(2)根据一次函数的增减性求出x的值,然后解答即可.
解答:解:(1)设A校运往C校的电脑为x台,则A校运往D校的电脑为(12-x)台,
从B校运往C校的电脑为(10-x)台,运往D校的电脑为8-(12-x)=(x-4)台,
由题意得,y=40x+80(12-x)+30(10-x)+50(x-4),
=-20x+1060,
由
解得4≤x≤10,
所以,y=-20x+1060(4≤x≤10);
(2)∵k=-20<0,
∴y随x的增大而减小,
∴当x=10时,y最小,
y最小=-20×10+1060=860元.
答:总运费最低方案:A校给C校10台,给D校2台,B校给C校0台,给D校6台,最低运费是860元.
从B校运往C校的电脑为(10-x)台,运往D校的电脑为8-(12-x)=(x-4)台,
由题意得,y=40x+80(12-x)+30(10-x)+50(x-4),
=-20x+1060,
由
|
所以,y=-20x+1060(4≤x≤10);
(2)∵k=-20<0,
∴y随x的增大而减小,
∴当x=10时,y最小,
y最小=-20×10+1060=860元.
答:总运费最低方案:A校给C校10台,给D校2台,B校给C校0台,给D校6台,最低运费是860元.
点评:本题考查了一次函数的应用,主要利用了一次函数的增减性求最值问题,难点在于表示出运往各校的电脑台数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若分式
有意义,则x的取值范围是( )
| 3 |
| x-1 |
| A、x≠-1 | B、x=1 |
| C、x≠1 | D、x=-1 |
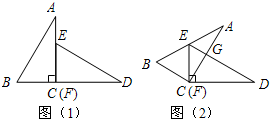 如图所示,已知△ACB△DFE与是两个全等的直角三角形,量得它们的斜边长为2cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B.C.F.D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则线段FG的长为( )
如图所示,已知△ACB△DFE与是两个全等的直角三角形,量得它们的斜边长为2cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B.C.F.D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则线段FG的长为( ) 如图,点A为双曲线y=-
如图,点A为双曲线y=-