题目内容
如图，篱笆（虚线部分）的长度是15cm，如何围篱笆才能使所围矩形的面积最大．考点：二次函数的最值
专题：
分析：设所围矩形的一边长为xcm，则另一边长可表示为（15-x）cm，那么其面积可表示成关于x的二次函数，根据二次函数的性质在定义域内求最大值即可．
解答：解：设所围矩形的一边长为xcm，则另一边长可表示为（15-x）cm，
则面积S=x（15-x）=-x2+15x=-（x-7.5）2+56.25，0＜x＜15，
当x=7.5时，面积S有最大值56.25．
答：当矩形的长与宽相等，都为7.5cm时，所围矩形的面积最大，最大值是56.25cm2．
则面积S=x（15-x）=-x2+15x=-（x-7.5）2+56.25，0＜x＜15，
当x=7.5时，面积S有最大值56.25．
答：当矩形的长与宽相等，都为7.5cm时，所围矩形的面积最大，最大值是56.25cm2．
点评：本题考查将实际问题求最值转化为二次函数在某个区间上的最值问题，二次函数求最值一般用配方法．
练习册系列答案
考前必练系列答案
相关题目
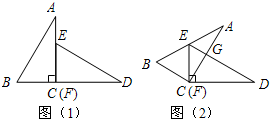如图所示，已知△ACB△DFE与是两个全等的直角三角形，量得它们的斜边长为2cm，较小锐角为30°，将这两个三角形摆成如图（1）所示的形状，使点B．C．F．D在同一条直线上，且点C与点F重合，将图（1）中的△ACB绕点C顺时针方向旋转到图（2）的位置，点E在AB边上，AC交DE于点G，则线段FG的长为（ ）
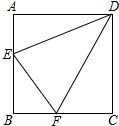在正方形ABCD中，∠EDF=45°，求证：EF=AE+CF．
如图，点A为双曲线y=-
如图，Rt△ABC的硬纸片，∠BAC=90°，AB=3，BC=5，AD为BC边上的高，从这张硬纸片剪下一个如图所示的内接正方形EFGH，则正方形EFGH的边长为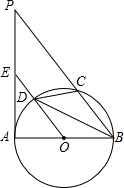
已知AB是⊙O的直径，PA是⊙O的切线，PB交⊙O于点C，过点O作OE∥PB，交⊙O于点D，交PA于点E．