题目内容
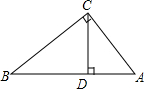如图，已知Rt△ABC中，∠C=90°，CD⊥AB于D，利用三角函数知识证明：（1）AC2=AD•AB；
（2）BC2=BD•AB；
（3）CD2=AD•BD；
（4）若AC=6，AD=3，利用（1）、（2）、（3）的结论求AB、BC、CD的长．
考点：解直角三角形
专题：
分析：（1）先由同角的余角相等可得∠ACD=∠B=90°-∠BCD，则sin∠ACD=sin∠B，再根据正弦函数的定义得出
=
，由比例的基本性质即可证明AC2=AD•AB；
（2）先由同角的余角相等可得∠BCD=∠A=90°-∠ACD，则sin∠BCD=sin∠A，再根据正弦函数的定义得出
=
，由比例的基本性质即可证明BC2=BD•AB；
（3）先根据正切函数的定义得出tan∠A=
=
，tan∠B=
=
，再将两式相乘得到
•
=
•
=1，即可证明CD2=AD•BD；
（4）先由（1）的结论可得AB=
=
12，于是BD=AB-AD=9，再根据（2）的结论得到BC2=BD•AB=9×12=108，那么BC=6
；然后根据（3）的结论得出CD2=AD•BD=3×9=27，于是CD=3
．
| AD |
| AC |
| AC |
| AB |
（2）先由同角的余角相等可得∠BCD=∠A=90°-∠ACD，则sin∠BCD=sin∠A，再根据正弦函数的定义得出
| BD |
| BC |
| BC |
| AB |
（3）先根据正切函数的定义得出tan∠A=
| CD |
| AD |
| BC |
| AC |
| CD |
| BD |
| AC |
| BC |
| CD |
| AD |
| CD |
| BD |
| BC |
| AC |
| AC |
| BC |
（4）先由（1）的结论可得AB=
| AC2 |
| AD |
| 62 |
| 3 |
| 3 |
| 3 |
解答：（1）证明：∵Rt△ABC中，∠C=90°，CD⊥AB于D，
∴∠ACD=∠B=90°-∠BCD，
∴sin∠ACD=sin∠B，
∴
=
，
∴AC2=AD•AB；
（2）证明：∵Rt△ABC中，∠C=90°，CD⊥AB于D，
∴∠BCD=∠A=90°-∠ACD，
∴sin∠BCD=sin∠A，
∴
=
，
∴BC2=BD•AB；
（3）证明：∵Rt△ABC中，∠C=90°，CD⊥AB于D，
∴tan∠A=
=
，tan∠B=
=
，
∴
•
=
•
=1，
∴CD2=AD•BD；
（4）解：∵AC=6，AD=3，
∴AB=
=
12；
∵BD=AB-AD=12-3=9，
∴BC2=BD•AB=9×12=108，
∴BC=6
；
∵CD2=AD•BD=3×9=27，
∴CD=3
．
∴∠ACD=∠B=90°-∠BCD，
∴sin∠ACD=sin∠B，
∴
| AD |
| AC |
| AC |
| AB |
∴AC2=AD•AB；
（2）证明：∵Rt△ABC中，∠C=90°，CD⊥AB于D，
∴∠BCD=∠A=90°-∠ACD，
∴sin∠BCD=sin∠A，
∴
| BD |
| BC |
| BC |
| AB |
∴BC2=BD•AB；
（3）证明：∵Rt△ABC中，∠C=90°，CD⊥AB于D，
∴tan∠A=
| CD |
| AD |
| BC |
| AC |
| CD |
| BD |
| AC |
| BC |
∴
| CD |
| AD |
| CD |
| BD |
| BC |
| AC |
| AC |
| BC |
∴CD2=AD•BD；
（4）解：∵AC=6，AD=3，
∴AB=
| AC2 |
| AD |
| 62 |
| 3 |
∵BD=AB-AD=12-3=9，
∴BC2=BD•AB=9×12=108，
∴BC=6
| 3 |
∵CD2=AD•BD=3×9=27，
∴CD=3
| 3 |
点评：本题考查了解直角三角形，余角的性质，比例的基本性质，掌握锐角三角函数的定义是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若分式
有意义，则x的取值范围是（ ）
| 3 |
| x-1 |
| A、x≠-1 | B、x=1 |
| C、x≠1 | D、x=-1 |
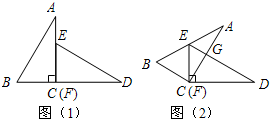如图所示，已知△ACB△DFE与是两个全等的直角三角形，量得它们的斜边长为2cm，较小锐角为30°，将这两个三角形摆成如图（1）所示的形状，使点B．C．F．D在同一条直线上，且点C与点F重合，将图（1）中的△ACB绕点C顺时针方向旋转到图（2）的位置，点E在AB边上，AC交DE于点G，则线段FG的长为（ ）
如图，点A为双曲线y=-
如图，在△ABC中，∠A=30°，CA=10cm，以C为圆心、半径为5cm的圆与AB是什么位置关系？