Question

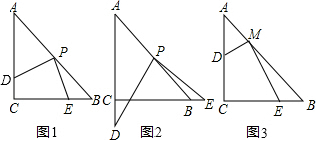
16．如图是一张直角三角形纸片，两直角边AC=6cm，BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，求DE的长．

Answer 1

分析 由勾股定理求出AB，由折叠的性质得出∠DEB=90°，AE=BE=$\frac{1}{2}$AB=5，在Rt△BDE中，由三角函数即可求出DE的长．

解答 解：∵∠C=90°，AC=6，BC=8，
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10，tanB=$\frac{AC}{BC}$=$\frac{6}{8}$=$\frac{3}{4}$，
由折叠的性质得：∠DEB=90°，AE=BE=$\frac{1}{2}$AB=5，
∴tanB=$\frac{DE}{BE}$=$\frac{3}{4}$，
∴DE=$\frac{3}{4}$BE=$\frac{3}{4}$×5=$\frac{15}{4}$（cm）．

点评 本题考查了翻折变换的性质、勾股定理、三角函数；熟练掌握翻折变换的性质，并能进行推理计算是解决问题的关键．