题目内容
5.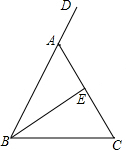 如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)连接CF,证明四边形ABCF是平行四边形.
分析 (1)根据角平分线的做法作图即可;
(2)首先证明AF∥BC,进而可得∠AFE=∠CBE,然后再证明△AEF≌△CEB,根据全等三角形的性质可得AF=BC,再利用一组对边平行且相等的四边形是平行四边形可得结论.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵AM平分∠DAC,
∴∠DAF=∠FAC=$\frac{1}{2}$∠DAC,
∵∠ABC+∠ACB=∠DAC,
∴∠ABC=∠ACB=$\frac{1}{2}$∠DAC,
∴∠DAF=∠ABC,
∴AF∥BC,
∴∠AFE=∠CBE,
∵E是AC的中点,
∴AE=EC,
在△AEF和△CEB中,
$\left\{\begin{array}{l}{∠AFE=∠EBC}\\{∠AEF=∠CEB}\\{AE=CE}\end{array}\right.$,
∴△AEF≌△CEB(AAS),
∴AF=BC,
∴四边形ABCF是平行四边形.
点评 此题主要考查了平行四边形的判定,以及全等三角形的判定与性质,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
15.把a3-4a分解因式正确的是( )
| A. | a(a2-4) | B. | a(a-2)2 | C. | a(a+2)(a-2) | D. | a(a+4)(a-4) |
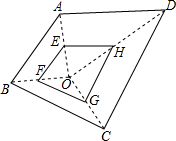 如图所示,E,F,G,H分别是OA,OB,OC,OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )
如图所示,E,F,G,H分别是OA,OB,OC,OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( ) 如图,A,B,C是⊙O上三点,已知∠ACB=α,则∠AOB=360°-2α.(用含α的式子表示)
如图,A,B,C是⊙O上三点,已知∠ACB=α,则∠AOB=360°-2α.(用含α的式子表示)