题目内容
6．
如图，在平行四边形ABCD中，∠BAD的平分线AE交DC于E，若DE=3，CE=2，求平行四边形ABCD的周长．
分析 由在平行四边形ABCD中，∠BAD的平分线AE交DC于E，易证得△ADE是等腰三角形，继而求得AD的长，然后由平行四边形的对边相等，求得答案．
解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，AD=BC，AB=CD=DE+CE=3+2=5，
∴∠AED=∠BAE，
∵AE平分∠BAD，
∴∠DAE=∠BAE，
∴∠DAE=∠AED，
∴AD=DE=3，
∴BC=AD=3，
∴平行四边形ABCD的周长为：AB+BC+CD+AD=5+3+5+3=16．
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质．注意证得△ADE是等腰三角形是关键．
练习册系列答案
名校课堂系列答案
相关题目
1．以下列各组数作为三角形的边长，能构成直角三角形的是（ ）
| A． | 4，5，6 | B． | 6，8，11 | C． | 1，1，$\sqrt{2}$ | D． | 5，12，23 |
如图，平行四边形ABCD的周长为20cm，AB≠AD，AC、BD相交于点O，EO⊥BD交AD于点E，则△ABE的周长为10cm．
18．已知x，y为实数，且|4x-y-2|+（2x+y-10）2=0，则（ ）
| A． | $\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-2}\\{y=-6}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=-6}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=6}\end{array}\right.$ |
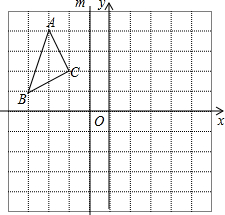在如图所示的正方形网格中，已知△ABC的三个顶点分别是格点A、B、C．