题目内容
5．
如图，在四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°，则∠DAB与∠BCD的数量关系是互补．
分析 连接AC．首先根据勾股定理求得AC的长，再根据勾股定理的逆定理求得∠D=90°即可．
解答 
解：连接AC．
∵AB=20，BC=15，∠B=90°，
∴由勾股定理，得AC2=202+152=625．
又CD=7，AD=24，
∴CD2十AD2=625，
∴AC2=CD2+AD2，
∴∠D=90°，
∴∠DAB与∠BCD的数量关系是互补，
故答案为：互补．
点评 本题考查了勾股定理、勾股定理的逆定理．熟练掌握勾股定理，由勾股定理的逆定理证明三角形是直角三角形是解决问题的关键．
练习册系列答案
相关题目
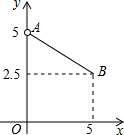如图是函数y=$\frac{1}{2}$x+5的一部分图象，利用图象回答下列问题：
如图，点A、B、C和点D、E、F分别在同一直线上，∠A=∠F，∠C=∠D，试说明∠α与∠β相等的理由．