题目内容
 如图,已知四边形ABCD中,∠D=∠C=90°,E为DC上一点,AE⊥BE,AE平分∠DAB,求证:以DC为直径的圆与AB相切.
如图,已知四边形ABCD中,∠D=∠C=90°,E为DC上一点,AE⊥BE,AE平分∠DAB,求证:以DC为直径的圆与AB相切.考点:切线的判定
专题:证明题
分析:作EF⊥AB于F,如图,由∠D=∠C=90°得到AD∥BC,根据平行线性质得∠BAD+∠ABC=90°,由于AE⊥BE,根据三角形内角和定理得到∠BAE+∠ABE=90°,则∠DAE+∠CBE=90°,根据AE平分∠DAB,得到∠BAE=∠DAE,ED=EF,所以∠ABE=∠CBE,再根据角平分线定理得到EF=EC,即有EF=ED=EC,然后根据切线的判定方法得到以DC为直径的圆与AB相切.
解答: 证明:作EF⊥AB于F,如图,
证明:作EF⊥AB于F,如图,
∵∠D=∠C=90°,
∴AD∥BC,
∴∠BAD+∠ABC=90°,
∵AE⊥BE,
∴∠BAE+∠ABE=90°,
∴∠DAE+∠CBE=90°,
∵AE平分∠DAB,
∴∠BAE=∠DAE,ED=EF,
∴∠ABE=∠CBE,
∴BE平分∠ABC,
∴EF=EC,
∴EF=ED=EC,
而EF⊥AB,
∴以DC为直径的圆与AB相切.
 证明:作EF⊥AB于F,如图,
证明:作EF⊥AB于F,如图,∵∠D=∠C=90°,
∴AD∥BC,
∴∠BAD+∠ABC=90°,
∵AE⊥BE,
∴∠BAE+∠ABE=90°,
∴∠DAE+∠CBE=90°,
∵AE平分∠DAB,
∴∠BAE=∠DAE,ED=EF,
∴∠ABE=∠CBE,
∴BE平分∠ABC,
∴EF=EC,
∴EF=ED=EC,
而EF⊥AB,
∴以DC为直径的圆与AB相切.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了角平分线定理.

练习册系列答案
相关题目
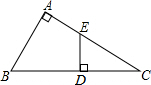 如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:AE=ED.
如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:AE=ED. 如图,在△ABC中,已知∠B=60°,∠C=45°,AB=2
如图,在△ABC中,已知∠B=60°,∠C=45°,AB=2