题目内容
18.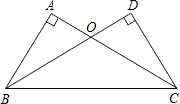 如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
分析 (1)利用“HL”证明Rt△ABC和Rt△DCB全等,根据全等三角形对应边相等可得AB=DC,然后利用“角角边”证明△ABO和△DCO全等即可;
(2)根据全等三角形对应边相等可得OB=OC,再根据等腰三角形的定义解答.
解答 (1)证明:在Rt△ABC和Rt△DCB中,
$\left\{\begin{array}{l}{BC=CB}\\{AC=BD}\end{array}\right.$,
∴Rt△ABC≌Rt△DCB(HL),
∴AB=DC,
在△ABO和△DCO中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠AOC=∠DOC}\\{AB=DC}\end{array}\right.$,
∴△ABO≌△DCO(AAS);
(2)解:△OBC是等腰三角形.
理由如下:∵△ABO≌△DCO,
∴OB=OC,
∴△OBC是等腰三角形.
点评 本题考查了全等三角形的判定与性质,等腰三角形的判定,先利用“HL”证明三角形全等是解题的关键,也是本题的难点.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
9.点M(-1,2)关于x轴对称的点的坐标为( )
| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (2,-1) |
3.下列各分式中最简分式是( )
| A. | $\frac{{a}^{2}-{b}^{2}}{(a+b)^{2}}$ | B. | $\frac{{b}^{2}-{a}^{2}}{a+b}$ | C. | $\frac{a+b}{a-b}$ | D. | $\frac{20(a-b)}{15(a+b)}$ |
10.在平面直角坐标系中,点A(-1,5),将点A向右平移2个单位、再向下平移3个单位得到点A1;再将线段OA1绕原点O顺时针旋转90°得到OA2.则A2的坐标为( )
| A. | (-1,2) | B. | (2,1) | C. | (2,-1) | D. | (3,-1) |
7.点P(5,-4)关于y轴对称点是( )
| A. | (5,4) | B. | (5,-4) | C. | (4,-5) | D. | (-5,-4) |
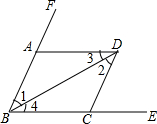 根据图填空,括号内填推理的依据.
根据图填空,括号内填推理的依据. 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,求∠DOE的度数.
如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,求∠DOE的度数.