题目内容
6. 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,求∠DOE的度数.
如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,求∠DOE的度数.
分析 根据角平分线的定义表示出∠COD和∠COE,再根据平角等于180°进行计算即可得解.
解答 解:∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠BOC,
∴∠DOE=∠COD+∠COE=$\frac{1}{2}$(∠AOC+∠BOC),
∵点A,O,B在同一条直线上,
∴∠AOC+∠BOC=180°,
∴∠DOE=$\frac{1}{2}$×180°=90°.
点评 本题考查了角平分线的定义,平角的定义,是基础题,熟记概念是解题的关键.

练习册系列答案
相关题目
16.两个相似多边形的面积之比是1:4,则这两个相似多边形的周长之比是( )
| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
17.下列计算正确的是( )
| A. | -(-2)2=22 | B. | (-3)2=6 | C. | -24=(-2)4 | D. | (-2)3=-23 |
14.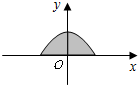 如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
 如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )| A. | 4 | B. | $\frac{16}{3}$ | C. | 2π | D. | 8 |
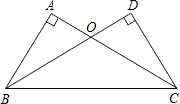 如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.