题目内容
13.如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+2交于C,D两点,其中点 C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.(1)求抛物线的解析式;
(2)若点P在直线BC上部的抛物线上运动,是否存在这样的点P,使得△PBC的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由.
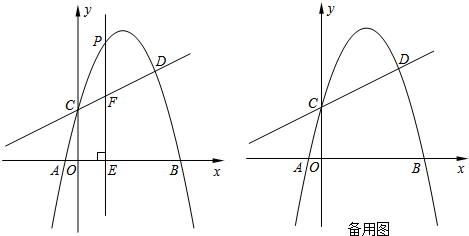
分析 (1)首先求出点C的坐标,然后利用待定系数法求出抛物线的解析式;
(2)如图2,连接PC,PB,BC,根据点P的横坐标为m,且点P在抛物上,得到点P的坐标为(m,-m2+$\frac{7}{2}$m+2),则PE=-m2+$\frac{7}{2}$m+2,OE=m,BE=4-m,OC=2,OB=4,根据S△PCB=S梯形OCPE+S△PBE-S△OBC确定二次函数,求得当m=2时有最值.
(3)本问采用数形结合的数学思想求解.将直线y=$\frac{1}{2}$x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值.
解答 解:(1)在直线解析式y=$\frac{1}{2}$x+2中,令x=0,得y=2,
∴C(0,2).
∵点C(0,2)、D(3,$\frac{7}{2}$)在抛物线y=-x2+bx+c上,
∴c=2,
-9+3b+c=$\frac{7}{2}$,
解得b=$\frac{7}{2}$,c=2,
∴抛物线的解析式为y=-${x}^{2}+\frac{7}{2}x+2$;
(2)如图2,连接PC,PB,BC,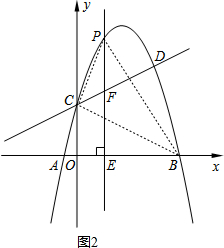
∵点P的横坐标为m,且点P在抛物线y=-${x}^{2}+\frac{7}{2}x$+2上,
∴点P的坐标为(m,-m2+$\frac{7}{2}$m+2),
当y=0时,即$-{x}^{2}+\frac{7}{2}x+2=0$,
解得:${x}_{1}=-\frac{1}{2},{x}_{2}=4$,
则PE=-m2+$\frac{7}{2}$m+2,OE=m,BE=4-m,OC=2,OB=4,
∴S△PCB=S梯形OCPE+S△PBE-S△OBC
=$\frac{1}{2}$[(PE+OC)•OE+BE•PE-OB•OC]
=$\frac{1}{2}$[(-m2+$\frac{7}{2}$m+2+2)•m+(-m2+$\frac{7}{2}$m+2+)(4-m)-2×4]
=-2m2+8m
=-2(m-2)2+8,
∴当m=2时,△PBC的面积最大;
(2)∵PF∥OC,且以O、C、P、F为顶点的四边形是平行四边形,
∴PF=OC=2,
∴将直线y=$\frac{1}{2}$x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
由答图1可以直观地看出,这样的交点有3个.
将直线y=$\frac{1}{2}$x+2沿y轴向上平移2个单位,得到直线y=$\frac{1}{2}$x+4
联立 $\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=-{x}^{2}+\frac{7}{2}x+2}\end{array}\right.$
解得x1=1,x2=2,
∴m1=1,m2=2;
将直线y=$\frac{1}{2}$x+2沿y轴向下平移2个单位,得到直线y=$\frac{1}{2}$x
联立 $\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=-{x}^{2}+\frac{7}{2}x+2}\end{array}\right.$
解得x3=$\frac{3+\sqrt{17}}{2}$,x4=$\frac{3-\sqrt{17}}{2}$(在y轴左侧,不合题意,舍去),
∴m3=$\frac{3+\sqrt{17}}{2}$,
∴当m为值为1,2或$\frac{3+\sqrt{17}}{2}$时,以O、C、P、F为顶点的四边形是平行四边形.
点评 本题是二次函数综合题型,考查了二次函数的图象与性质、一次函数的图象与性质、解方程(方程组)、平行四边形、相似三角形、勾股定理等重要知识点.第(2)问采用数形结合思想求解,直观形象且易于理解.

 如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.
如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.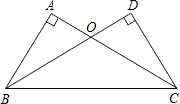 如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.