Question

6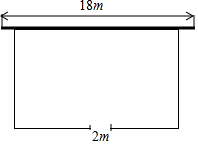．如图，若要建一个长方形鸡场，鸡场的一边靠墙，墙对面有一个2米宽的门，另三边用竹篱笆围成，篱笆总长33米．
（1）若墙长为18米，要围成鸡场的面积为150平方米，则鸡场的长和宽各为多少米？
（2）围成鸡场的面积可能达到200平方米吗？

Answer 1

分析 （1）若鸡场面积150平方米，求鸡场的长和宽，关键是用一个未知数表示出长或宽，并注意去掉门的宽度；
（2）求二次函数的最值问题，因为a＜0，所以当（x-$\frac{35}{4}$）²=0时函数式有最大值．

解答 解：（1）设宽为x米，则：x（33-2x+2）=150，
解得：x₁=10，x₂=$\frac{15}{2}$（不合题意舍去），
∴长为15米，宽为10米；

（2）设面积为w平方米，则：W=x（33-2x+2），
变形为：W=-2（x-$\frac{35}{4}$）²+$\frac{1225}{8}$
故鸡场面积最大值为$\frac{1225}{8}$＜200，即不可能达到200平方米．

点评 此题主要考查了一元二次方程的应用，一面靠墙矩形面积求法，以及二次函数最值问题，题目比较典型，是中考中热点问题．