题目内容
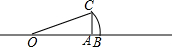如图，在数轴上画出表示| 10 |
| 10 |
作法：如图，在数轴上找到点A，使OA=
| 10 |
考点：勾股定理,实数与数轴
专题：
分析：根据
=
画出图形即可．
| 10 |
| 32+12 |
解答：解：∵
=
，
∴长为
的线段是直角边为正整数3，1的直角三角形的斜边，
∴在数轴上找到点A，使OA=3，作AC⊥OA且截取AC=1，以O为圆心，以OC为半径作弧，弧与数轴的交点B表示的数即为
．．
故答案为：3，1，3，1．
| 10 |
| 32+12 |
∴长为
| 10 |
∴在数轴上找到点A，使OA=3，作AC⊥OA且截取AC=1，以O为圆心，以OC为半径作弧，弧与数轴的交点B表示的数即为
| 10 |
故答案为：3，1，3，1．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
如图，要测量池塘两端A，B的距离，先在平面上取一个可以直接到达A，B的点C，连接AC并延长到D，使AC=3CD，连接BC并延长到E，使BC=3CE，连接DE，测得DE=13m，那么池塘的宽AB是多少？
王刚将一副三角板如图所示摆在一起，若已知CD=2，AB=
在△ABC中，AB=AC=17，BC=16，求S△ABC．
已知，如图，∠A=∠ACE，∠B=∠BDF，且∠A=∠B，求证：EC∥DF．
已知：如图，OB是∠AOC的角平分线，OC是∠AOD的角平分线，∠COD=70°，那么∠AOD的度数为