题目内容
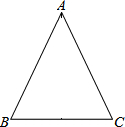 在△ABC中,AB=AC=17,BC=16,求S△ABC.
在△ABC中,AB=AC=17,BC=16,求S△ABC.考点:勾股定理,等腰三角形的性质
专题:
分析:利用等腰三角形的性质求得BD=
BC=8cm.然后在直角△ABD中,利用勾股定理来求AD的长度,进而可求出三角形的面积.
| 1 |
| 2 |
解答:解:如图,作AD⊥BC于点D,
∵△ABC中,AB=AC=17,BC=16,
∴BD=
BC=8,
∴在直角△ABD中,由勾股定理,得
AD=
=15,
∴S△ABC=
×15×8=60.

∵△ABC中,AB=AC=17,BC=16,
∴BD=
| 1 |
| 2 |
∴在直角△ABD中,由勾股定理,得
AD=
| 172-82 |
∴S△ABC=
| 1 |
| 2 |
点评:此题主要考查了勾股定理,等腰三角形的性质的理解及运用.利用等腰三角形“三线合一”的性质求得AD的长度是解题的关键.

练习册系列答案
相关题目
下面的式子成立的是 ( )
| A、7ab-7ba=0 |
| B、5y2-2y2=3 |
| C、4x2y-5y2x=-x2y |
| D、a+a=2a2 |
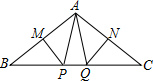 如图,△ABC中,MP和NQ分别垂直平分AB和AC,若∠PAQ=40°,则∠BAC的度数是( )
如图,△ABC中,MP和NQ分别垂直平分AB和AC,若∠PAQ=40°,则∠BAC的度数是( )| A、140° | B、110° |
| C、100° | D、70° |
 如图,点O(0,0),A(2,2),若存在格点P,使△APO为等腰直角三角形,则点P的个数为( )
如图,点O(0,0),A(2,2),若存在格点P,使△APO为等腰直角三角形,则点P的个数为( )| A、4 | B、5 | C、6 | D、8 |
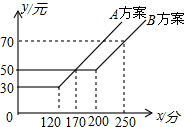 某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题:
某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题: 如图,在数轴上画出表示
如图,在数轴上画出表示