题目内容
如图，要测量池塘两端A，B的距离，先在平面上取一个可以直接到达A，B的点C，连接AC并延长到D，使AC=3CD，连接BC并延长到E，使BC=3CE，连接DE，测得DE=13m，那么池塘的宽AB是多少？考点：相似三角形的应用
专题：
分析：利用相似三角形的判定定理“两边及夹角法”推知△ABC∽△DEC，则其对应边成比例．由此求得AB的长度．
解答：解：∵AC=3CD，BC=3CE，
∴
=
=3．
又∵∠ACB=∠DCE，
∴△ABC∽△DEC，
∴
=
=3．
∴AB=3DE=39cm．
即池塘的宽AB是39cm．
∴
| AC |
| CD |
| BC |
| CE |
又∵∠ACB=∠DCE，
∴△ABC∽△DEC，
∴
| AB |
| ED |
| BC |
| CE |
∴AB=3DE=39cm．
即池塘的宽AB是39cm．
点评：本题考查了相似三角形的应用．解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
图中两个四边形是位似图形，则它们的位似中心是（ ）| A、点M | B、点N | C、点O | D、点P |
如图所示，这是一个由小立方块塔成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数，它的左视图是（ ）
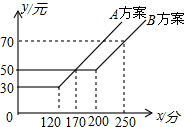某电信公司提供了A，B两种通讯方案，其通讯费用y（元）与通话时间x（分）之间的关系如图所示，观察图象，回答下列问题：
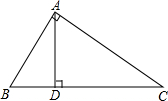在△ABC中，∠BAC=90°，AD⊥BC于点D，若AB=30cm，BC=50cm，求线段CD的长．
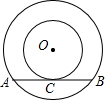半径为5的大⊙O的弦与小⊙O相切于点C，且AB=8，则小⊙O的半径为
如图，一场暴雨过后，垂直于地面的一棵树在距地面2m处折断，树尖B恰好碰到地面，经测量AB=4m，则树高为（ ）A、2
| ||
B、2
| ||
C、（2
| ||
| D、4m |
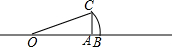如图，在数轴上画出表示