题目内容
20.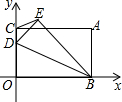 如图,将一矩形OBAC放在平面直角坐标系中,O为原点,点B,C分别在x轴、y轴上,点A(4,3),点D为线段OC上一动点,将△BOD沿BD翻折,点O落在点E处,连CE,则CE的最小值为1,此时点D的坐标为(0,$\frac{4}{3}$).
如图,将一矩形OBAC放在平面直角坐标系中,O为原点,点B,C分别在x轴、y轴上,点A(4,3),点D为线段OC上一动点,将△BOD沿BD翻折,点O落在点E处,连CE,则CE的最小值为1,此时点D的坐标为(0,$\frac{4}{3}$).
分析 当C、E、B共线时,EC最小,此时EC=BC-BE=BC-BO,设OD=DE=x,在RT△CDE中利用勾股定理,列出方程即可解决问题.
解答 解:如图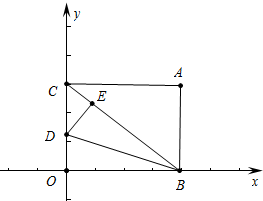 ,当C、E、B共线时,EC最小,此时EC=BC-BE=BC-BO,
,当C、E、B共线时,EC最小,此时EC=BC-BE=BC-BO,
在RT△OBC中,∵∠BOC=90°,BO=4,OC=3,
∴BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵EC最小值=BC-BO=5-4=1,
设OD=DE=x,
在RT△CDE中,∵∠CED=90°,CD=3-x,DE=x,CE=1,
∴(3-x)2=x2+12,
∴x=$\frac{4}{3}$,
∴点D坐标为(0,$\frac{4}{3}$).
故答案分别为1,(0,$\frac{4}{3}$).
点评 本题考查矩形的性质、坐标与图形性质、翻折变换等知识,解题的关键是正确寻找点E位置,学会利用勾股定理构建方程解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知x>0,且(x-1)2-324=0,则x+1的值为( )
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
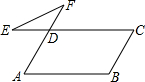 如图,在?ABCD中,∠B=120°,延长CD至点E,延长AD至点F,连结EF,则∠E+∠F=60度.
如图,在?ABCD中,∠B=120°,延长CD至点E,延长AD至点F,连结EF,则∠E+∠F=60度. 如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上.
如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上. 将两个完全一样的三角板按如图位置放在一起,就可以画出两条相互平行的直线,这样画图的原理是内错角相等,两直线平行.
将两个完全一样的三角板按如图位置放在一起,就可以画出两条相互平行的直线,这样画图的原理是内错角相等,两直线平行.