题目内容
13.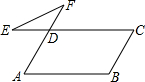 如图,在?ABCD中,∠B=120°,延长CD至点E,延长AD至点F,连结EF,则∠E+∠F=60度.
如图,在?ABCD中,∠B=120°,延长CD至点E,延长AD至点F,连结EF,则∠E+∠F=60度.
分析 由在?ABCD中,∠B=120°,可求得∠A的度数,继而求得∠FDC的度数,然后由三角形的外角的性质,求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠FDC=∠A=180°-∠B=180°-120°=60°,
∴∠E+∠F=∠FDC=60°.
故答案为:60.
点评 此题考查了平行四边形的性质以及三角形外角的性质.注意平行四边形的对角相等,邻角互补.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
2.小明在下面的计算中只做对了一道题,他做对的题目是( )
| A. | ($\frac{a}{b}$)2=$\frac{{a}^{2}}{b}$ | B. | $\frac{1}{a}+\frac{1}{b}=\frac{2}{a+b}$ | C. | $\frac{{x}^{2}-{y}^{2}}{x-y}=x+y$ | D. | $\frac{-x-y}{x-y}=-1$ |
9.下列各组线段中,不能够组成直角三角形的一组是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 2,3,4 |
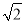 ,BM=2,则MN的长为_______.
,BM=2,则MN的长为_______.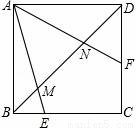
 如图,在矩形ABCD中,AC与BD交于点O,DE∥AC,CE∥BD.
如图,在矩形ABCD中,AC与BD交于点O,DE∥AC,CE∥BD.
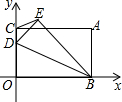 如图,将一矩形OBAC放在平面直角坐标系中,O为原点,点B,C分别在x轴、y轴上,点A(4,3),点D为线段OC上一动点,将△BOD沿BD翻折,点O落在点E处,连CE,则CE的最小值为1,此时点D的坐标为(0,$\frac{4}{3}$).
如图,将一矩形OBAC放在平面直角坐标系中,O为原点,点B,C分别在x轴、y轴上,点A(4,3),点D为线段OC上一动点,将△BOD沿BD翻折,点O落在点E处,连CE,则CE的最小值为1,此时点D的坐标为(0,$\frac{4}{3}$).