题目内容
2.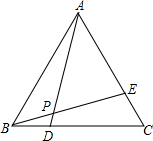 如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )
如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先根据SAS定理得出△ABD≌△BCE,结合全等三角形的性质进行判断.
解答  解:①因为AC=BC,BD=CE,所以AE=CD.故正确
解:①因为AC=BC,BD=CE,所以AE=CD.故正确
②∵△ABC是等边三角形,
∴∠ABD=∠C=60°,AB=BC.
在△ABD与△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS);
∴AD=BE.
故正确;
③由②知△ABD≌△BCE,所以∠ADB=∠CEB,则∠AEB=∠ADC,故正确;
④∵由②知△ABD≌△BCE.
∴∠BAD=∠EBC,
∴∠BAD+∠ABP=∠ABD=60°.
∵∠APE是△ABP的外角,
∴∠APE=∠BAD+∠ABP=60°.
故正确.
综上所述,正确的结论有4个.
故选:D.
点评 本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.

练习册系列答案
相关题目
14.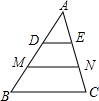 如图,在△ABC中,D、M在AB上,E、N在AC上且AD=DM=MB,AE=EN=NC,△ADE、梯形DMNE、梯形MBCN的面积比为( )
如图,在△ABC中,D、M在AB上,E、N在AC上且AD=DM=MB,AE=EN=NC,△ADE、梯形DMNE、梯形MBCN的面积比为( )
 如图,在△ABC中,D、M在AB上,E、N在AC上且AD=DM=MB,AE=EN=NC,△ADE、梯形DMNE、梯形MBCN的面积比为( )
如图,在△ABC中,D、M在AB上,E、N在AC上且AD=DM=MB,AE=EN=NC,△ADE、梯形DMNE、梯形MBCN的面积比为( )| A. | 1:2:3 | B. | 1:4:9 | C. | 1:3:5 | D. | 1:3:7 |
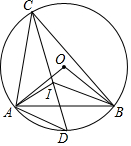 如图,△ABC的外接圆为⊙O,I为△ABC的内心,∠ACB=50°,CI的延长线交⊙O于点D.
如图,△ABC的外接圆为⊙O,I为△ABC的内心,∠ACB=50°,CI的延长线交⊙O于点D.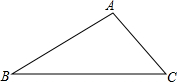 如图,在△ABC中,已知∠B=30°,∠C=45°,AB=6,AC=3$\sqrt{2}$,求BC的长.
如图,在△ABC中,已知∠B=30°,∠C=45°,AB=6,AC=3$\sqrt{2}$,求BC的长.