题目内容
6.用适当的方法解下列方程:(1)2x2-8x=0.
(2)x2-3x-4=0.
求出抛物线的开口方向、对称轴、顶点坐标.
(3)y=$\frac{1}{2}$x2-x+3(公式法).
分析 (1)利用因式分解法求解即可;
(2)利用因式分解法求解即可;
(3)利用顶点坐标公式求解.
解答 解:
(1)原方程可化为x2-4x=0,
因式分解可得x(x-4)=0,
∴x=0或x-4=0,
∴x1=0,x2=4;
(2)因式分解可得(x-4)(x+1)=0,
∴x-4=0或x+1=0,
∴x1=4,x2=-1;
(3)在y=$\frac{1}{2}$x2-x+3中,
∵a=$\frac{1}{2}$>0,
∴抛物线开口向上,
∵-$\frac{b}{2a}$=-$\frac{-1}{2×\frac{1}{2}}$=1,$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×\frac{1}{2}×3-(-1)^{2}}{4×\frac{1}{2}}$=$\frac{5}{2}$,
∴抛物线对称轴为x=1,顶点坐标为(1,$\frac{5}{2}$).
点评 本题主要考查一元二次方程的解法及二次函数的性质,掌握因式分解的方法及二次函数的顶点式是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 某农场要建一个面积为80m2长方形的养鸡场,鸡场的一边靠墙(墙长15m),另外三边用木栏围成,木栏长26m,求养鸡场的长和宽各是多少?
某农场要建一个面积为80m2长方形的养鸡场,鸡场的一边靠墙(墙长15m),另外三边用木栏围成,木栏长26m,求养鸡场的长和宽各是多少?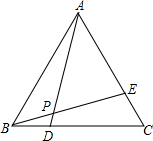 如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )
如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )