题目内容
如图，在△ABC中，点C，F分别在上BD、AB上．AC、DF相交于E．若CD=2BC，AE=2CE，则DE：EF=考点：平行线分线段成比例
专题：计算题
分析：过C点作CH∥DF交AB于H，如图，关键平行线分线段成比例定理，由EF∥CH得
=
=
，则EF=
CH；由CH∥DF得到
=
=
，则DF=3CH，所以
=
，然后根据比例的性质可得
=
．
| EF |
| CH |
| AE |
| AC |
| 2 |
| 3 |
| 2 |
| 3 |
| CH |
| DF |
| BC |
| BD |
| 1 |
| 3 |
| DF |
| EF |
| 9 |
| 2 |
| DE |
| EF |
| 7 |
| 2 |
解答：解：过C点作CH∥DF交AB于H，如图，
∵EF∥CH，
∴
=
=
=
=
，
∴EF=
CH，
∵CH∥DF，
∴
=
=
=
=
，
∴DF=3CH，
∴
=
=
，
∴
=
，
即
=
．
故答案为7：2．
∵EF∥CH，
∴
| EF |
| CH |
| AE |
| AC |
| AE |
| AE+CE |
| 2CE |
| 2CE+CE |
| 2 |
| 3 |
∴EF=
| 2 |
| 3 |
∵CH∥DF，
∴
| CH |
| DF |
| BC |
| BD |
| BC |
| BC+CD |
| BC |
| BC+2BC |
| 1 |
| 3 |
∴DF=3CH，
∴
| DF |
| EF |
| 3CH | ||
|
| 9 |
| 2 |
∴
| DF-EF |
| EF |
| 9-2 |
| 2 |
即
| DE |
| EF |
| 7 |
| 2 |
故答案为7：2．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．本题的关键是作平行线，构造平行线分线段成比例定理的图形．
练习册系列答案
阅读快车系列答案
相关题目
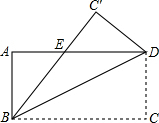如图，将长方形ABCD沿BD对折，C点落在C′的位置，BC′与AD交于点E．
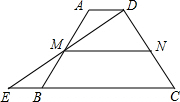如图，在梯形ABCD中，AD∥BC，延长CB到点E，使BE=AD，连接DE交AB于点M
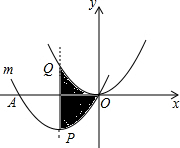如图，把抛物线y=x2平移得到抛物线m，抛物线m经过点A（-4，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y=x2交于点Q，则图中阴影部分的面积为