题目内容
当0≤x≤2时,函数y=x2+(m-3)x+m的图象与x轴有两个不同的公共点,求m的取值范围.
考点:抛物线与x轴的交点
专题:
分析:当0≤x≤2时,函数与x轴有两个不同的交点则有:①根的判别式△>0;②由于抛物线开口向上,所以当x=0和x=2时,y值应具备:y≥0;
(可结合图象进行判断,当x取0、2时,函数图象均在x轴或x轴上方.);③抛物线的对称轴在0~2的范围内,不包括0和2;
(若取0或2,那么在0≤x≤2的区间内,函数与x轴不会有两个不同的交点.)根据上述三个条件即可确定m的取值范围.
(可结合图象进行判断,当x取0、2时,函数图象均在x轴或x轴上方.);③抛物线的对称轴在0~2的范围内,不包括0和2;
(若取0或2,那么在0≤x≤2的区间内,函数与x轴不会有两个不同的交点.)根据上述三个条件即可确定m的取值范围.
解答:解:
当0≤x≤2时,函数y=x2+(m-3)x+m的图象与x轴有两个不同的交点,
∴m应同时满足下列三个方面的条件:
方程x2+(m-3)x+m=0的判别式△=(m-3)2-4m=(m-1)(m-9)>0,
抛物线y=x2+(m-3)x+m的对称轴满足0<
<2,
当x=0时,函数值y=m≥0,
当x=2时,函数值y=3m-2≥0,
即
,解得
≤m<1;
∴当
≤m<1时,函数图象y=x2+(m-2)x+3(0≤x≤2)与x轴有两个不同交点.
当0≤x≤2时,函数y=x2+(m-3)x+m的图象与x轴有两个不同的交点,
∴m应同时满足下列三个方面的条件:
方程x2+(m-3)x+m=0的判别式△=(m-3)2-4m=(m-1)(m-9)>0,
抛物线y=x2+(m-3)x+m的对称轴满足0<
| 3-m |
| 2 |
当x=0时,函数值y=m≥0,
当x=2时,函数值y=3m-2≥0,
即
|
| 2 |
| 3 |
∴当
| 2 |
| 3 |
点评:本题主要考查二次函数与x的交点,掌握二次函数与x轴有两个交点的条件是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AC=
如图,AC=| 1 |
| 3 |
| 1 |
| 4 |
| A、1:6 | B、1:8 |
| C、1:12 | D、1:16 |
 甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )
甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )| A、甲的速度是5km/h |
| B、乙的速度是20km/h |
| C、乙比甲晚出发1h |
| D、甲走完全程比乙走完全程多用了2h |
若∠A=12°12′,∠B=20°15′30″,∠C=20.25°,则( )
| A、∠A>∠B>∠C |
| B、∠B>∠C>∠A |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
从O点看,射线OA在是北偏西60°方向上,射线OB在南偏东15°方向上,那么∠AOB的度数为( )
| A、45° | B、75° |
| C、90° | D、135° |
 如图,在△ABC中,点C,F分别在上BD、AB上.AC、DF相交于E.若CD=2BC,AE=2CE,则DE:EF=
如图,在△ABC中,点C,F分别在上BD、AB上.AC、DF相交于E.若CD=2BC,AE=2CE,则DE:EF=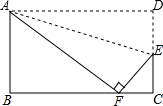 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF=
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF=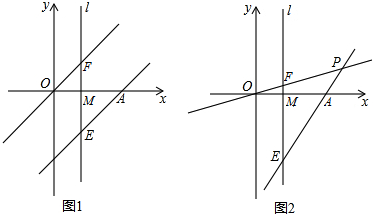
 如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,
如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,