题目内容
计算 的结果是( )
的结果是( )
A. 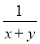 B.
B. 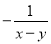 C.
C. 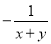 D.
D. 
 D
【解析】试题分析:原式=
=
=
=.
故选D.
D
【解析】试题分析:原式=
=
=
=.
故选D.
(吉安永新县期末)如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
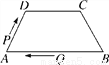
A. 4s B. 3s C. 2s D. 1s
 B
【解析】试题解析:设运动时间为t秒,则CP=12-3t,BQ=t,
根据题意得到12-3t=t,
解得:t=3,
故选B.
B
【解析】试题解析:设运动时间为t秒,则CP=12-3t,BQ=t,
根据题意得到12-3t=t,
解得:t=3,
故选B. 把分式 中的m和n都扩大4倍,那么分式的值( )
中的m和n都扩大4倍,那么分式的值( )
A. 也扩大4倍 B. 扩大为原来的4倍 C. 不变 D. 缩小为原来的
 C
【解析】试题分析:把分式中的m、n分别用4m、4n代替,
得==,
所以分式的值不变,
故选C.
C
【解析】试题分析:把分式中的m、n分别用4m、4n代替,
得==,
所以分式的值不变,
故选C. 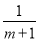 与
与 的最简公分母是__________
的最简公分母是__________
 【解析】试题分析:m2-1=(m+1)(m-1),
所以最简公分母是m2-1.
故答案为:m2-1.
【解析】试题分析:m2-1=(m+1)(m-1),
所以最简公分母是m2-1.
故答案为:m2-1. 下列各式与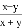 相等的是( )
相等的是( )
A. 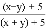 B.
B. 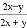
C. 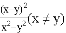 D.
D. 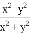
 C
【解析】试题分析:因为不能约分,所以,所以A错误;因为不能约分,所以,所以B错误;因为,所以C正确;因为不能约分,所以,所以D错误;故选:C.
C
【解析】试题分析:因为不能约分,所以,所以A错误;因为不能约分,所以,所以B错误;因为,所以C正确;因为不能约分,所以,所以D错误;故选:C. 某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过105700元购进40台电脑,其中A型电脑每台进价2500元,B型电脑每台进价2800元,A型每台售价3000元,B型每台售价3200元,预计销售额不低于123200元.设A型电脑购进x台、商场的总利润为y(元).
(1)请你设计出进货方案;
(2)求出总利润y(元)与购进A型电脑x(台)的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?
(3)商场准备拿出(2)中的最大利润的一部分再次购进A型和B型电脑至少各两台,另一部分为地震灾区购买单价为500元的帐篷若干顶.在钱用尽三样都购买的前提下请直接写出购买A型电脑、B型电脑和帐篷的方案.
 【解析】
(1)设A型电脑购进x台,则B型电脑购进(40﹣x)台,由题意,得
,解得:21≤x≤24。
∵x为整数,∴x=21,22,23,24。
∴有4种购买方案:
方案1:购A型电脑21台,B型电脑19台;
方案2:购A型电脑22台,B型电脑18台;
方案3:购A型电脑23台,B型电脑17台;
方案4:购A型电脑24台,B型电脑16台。
(2)...
【解析】
(1)设A型电脑购进x台,则B型电脑购进(40﹣x)台,由题意,得
,解得:21≤x≤24。
∵x为整数,∴x=21,22,23,24。
∴有4种购买方案:
方案1:购A型电脑21台,B型电脑19台;
方案2:购A型电脑22台,B型电脑18台;
方案3:购A型电脑23台,B型电脑17台;
方案4:购A型电脑24台,B型电脑16台。
(2)... 有一个两位数,其个位数字比十位数字大2,已知这个两位数大于20且小于40,那么这个两位数是__.
 24或35
【解析】【解析】
设这个两位数十位数字为x,则个位数字为x+2,那么这个两位数为10x+x+2.根据题意得:
,解得: .
∵x为正整数,∴x为2或3,
∴10x+x+2=24或35,
则这个两位数是24或35.
故答案为:24或35.
24或35
【解析】【解析】
设这个两位数十位数字为x,则个位数字为x+2,那么这个两位数为10x+x+2.根据题意得:
,解得: .
∵x为正整数,∴x为2或3,
∴10x+x+2=24或35,
则这个两位数是24或35.
故答案为:24或35. 如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,AC∥DE,延长CA交射线EB于点G,点F恰好是AD中点。
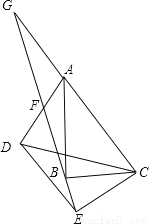
(1)求证:△AFG≌△DFE;
(2)若BC=CE,
①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
 (1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A...
(1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A... 已知三角形的两边为3和4,则第三边a的取值范围是________.
 1<a<7
【解析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,得4-3<a<4+3,即1<a<7.
故答案为:1<a<7.
1<a<7
【解析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,得4-3<a<4+3,即1<a<7.
故答案为:1<a<7. 
