题目内容
14.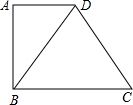 如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )
如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
分析 根据等边三角形性质得出DB=DC=BC=8cm,∠DBC=60°,求出∠ABD=30°,求出AD=$\frac{1}{2}$BD=4cm,代入梯形ABCD的中位线$\frac{1}{2}$(AD+BC)求出即可
解答 解:∵△DBC是等边三角形,
∴DB=DC=BC=8cm,∠DBC=60°,
∵∠ABC=90°,
∴∠ABD=30°,
∵∠A=90°,
∴AD=$\frac{1}{2}$BD=4cm,
∴梯形ABCD的中位线是$\frac{1}{2}$(AD+BC)=$\frac{1}{2}$×(4cm+8cm)=6cm,
故选B.
点评 本题考查了等边三角形性质,直角梯形,梯形的中位线的应用,关键是求出AD和BC的长.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
5.等腰梯形底角为α,以腰长为直径作圆与另一腰切于M,交较长底边AB于E,则$\frac{BE}{AE}$的值为( )
| A. | 2sinαcosα | B. | sinα | C. | cosα | D. | cos2α |
9.若关于x的方程x2-2x+a=3的解为x=-2,则字母a的值为( )
| A. | 3 | B. | 5 | C. | -5 | D. | 11 |
6.如果一个角的两边分别平行于另一个角的两边,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 无法确定 |
 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: