题目内容
 海上有一座灯塔P,一客轮以60海里/时的速度由西向东航行,行至A处时测得灯塔P在北偏东60°方向,继续航行40分钟后,到B处又测得灯塔P在北偏东30°方向.
海上有一座灯塔P,一客轮以60海里/时的速度由西向东航行,行至A处时测得灯塔P在北偏东60°方向,继续航行40分钟后,到B处又测得灯塔P在北偏东30°方向.(1)客轮在B处距离灯塔P多少海里?
(2)若在灯塔周围30海里有暗礁,客轮继续向东航行是否由触礁危险?
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)作PH⊥AC于点H,根据等腰三角形的判定与性质,可得AB=BP,再根据路程=速度×时间即可求出客轮在B处距离灯塔P的长;
(2)本题实际上是问,P到AB的距离即CD是否大于30,如果大于则无触礁危险,反之则有,根据三角函数可求PH的值,进行比较即可求解.
(2)本题实际上是问,P到AB的距离即CD是否大于30,如果大于则无触礁危险,反之则有,根据三角函数可求PH的值,进行比较即可求解.
解答: 解:(1)作PH⊥AC于点H
解:(1)作PH⊥AC于点H
由题意可知∠PAB=30°,∠PBC=60°,
∴∠PAB=∠APB=30°,
∴AB=BP=60×
=40海里.
∴客轮在B距灯塔40海里.
(2)由题意可知∠BPH=30°,
∵cos∠BPH=
=
∴
=
∴PH=20
≈34.64
∵34.64>30
∴客轮继续向东航行无触礁危险.
 解:(1)作PH⊥AC于点H
解:(1)作PH⊥AC于点H由题意可知∠PAB=30°,∠PBC=60°,
∴∠PAB=∠APB=30°,
∴AB=BP=60×
| 2 |
| 3 |
∴客轮在B距灯塔40海里.
(2)由题意可知∠BPH=30°,
∵cos∠BPH=
| PH |
| BP |
| ||
| 2 |
∴
| PH |
| BP |
| ||
| 2 |
∴PH=20
| 3 |
∵34.64>30
∴客轮继续向东航行无触礁危险.
点评:考查了解直角三角形的应用-方向角问题,本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
比0大的数是( )
| A、-2 | ||
B、-
| ||
| C、0 | ||
| D、0.001 |
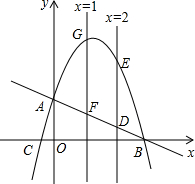 如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+
如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+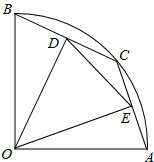 【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
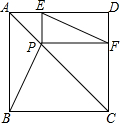 如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足,
如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足, 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为67°,在教学楼三楼D处测得旗杆顶部的仰角为37°,旗杆底部与教学楼一楼在同一水平线上,已知每层的高度为3m,求旗杆AB的高度(精确到0.1m).(参考数据:tan67°≈
某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为67°,在教学楼三楼D处测得旗杆顶部的仰角为37°,旗杆底部与教学楼一楼在同一水平线上,已知每层的高度为3m,求旗杆AB的高度(精确到0.1m).(参考数据:tan67°≈ 如图,在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
如图,在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧