Question

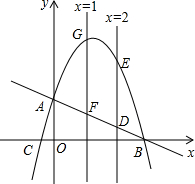如图，抛物线与x轴相交于B、C两点，与y轴相交于点A，P（a，-a²+

7

2

a+m）（a为任意实数）在抛物线上，直线y=kx+b经过A、B两点，平行于y轴的直线x=2交直线AB于点D，交抛物线于点E．
（1）若m=2，
①求直线AB的解析式；
②直线x=t（0≤t≤4）与直线AB相交于点F，与抛物线相交于点G．若FG：DE=3：4，求t的值；
（2）当EO平分∠AED时，求m的值．

Answer 1

考点：二次函数综合题

专题：

分析：（1）根据点P的坐标，可得出抛物线解析式，然后求出A、B、C的坐标，利用待定系数法求出直线AB的解析式；
（2）①根据点E（2，5），D（2，1），G（t，-t²+

7

2

t+2），F（t，-t+2），表示出DE、FG，再由FG：DE=3：4，可得出t的值；
②设点A（0，2+m），则点E（2，3+m），过点O作OM⊥AE交直线AE于点M，根据EO平分∠AED及平行线的性质可推出∠AEO=∠AOE，AO=AE，继而可得出m的值．

解答：解：（1）①∵P（a，-a²+

7

2

a+m）（a为任意实数）在抛物线上，
∴y=-x²+

7

2

x+m，
当m=2时，则y=-x²+

7

2

x+2，
∴A坐标为（0，2），B坐标为（4，0）C坐标为（-

1

2

，0），
将点A、B的坐标代入y=kx+b，得：

4k+b=0 b=2

，
解得：

k=- 1 2 b=2

，
∴直线AB的解析式为y=-

1

2

x+2；
②∵F为（t，2-

1

2

t）G为（t，-t²+

7

2

t+2），E为（2，5），D为（2，1）
∴FG=t²+

7

2

t+2）-（2-

1

2

）=-t²+4t，DE=4，
∵FG：DE=3：4，
∴-t²+4t=3，
解得t₁=1，t₂=3；

（2）过点O作OM⊥AE交直线AE于点M，由题意得OM=X_E=2，E的坐标为（2，m+3），
∵直线AE的解析式为y=

3

2

x+m，
∴OA=m，OM=

2 13

13

m=2，得m=

13

，
∴m的值为

13

．

点评：本题考查了二次函数的综合，涉及了待定系数法求函数解析式、平行线的性质及等腰三角形的判定与性质，本题的突破口在于根据点P的坐标得出抛物线解析式，同学们注意培养自己解答综合题的能力，将所学知识融会贯通．