题目内容
13. 如图,已知三角形三个顶点的坐标分别为:A(2,-1),B(4,3),C(1,2),请你计算△ABC的面积.
如图,已知三角形三个顶点的坐标分别为:A(2,-1),B(4,3),C(1,2),请你计算△ABC的面积.
分析 根据图形割补法,可得矩形BDEF,根据面积的和差,可得答案.
解答 解:如图: ,
,
由A(2,-1),B(4,3),C(1,2),得
BD=4-1=3,CD=3-2=1,CE=2-(-1)=3,AE=2-1=1,AF=4-2=2,BF=3-(-1)=4.
S△ABC=S矩形BDEF-S△BDC-S△ACE-S△ABF
=BD•BF-$\frac{1}{2}$DC•DB-$\frac{1}{2}$AE•CE-$\frac{1}{2}$AF•BF
=3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4
=12-$\frac{3}{2}$-$\frac{3}{2}$-4
=5.
点评 本题考查了坐标与图形的性质,利用图形割补法是求面积的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
3. 已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
 已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )| A. | a>b | B. | ab<0 | C. | b-a>0 | D. | a+b>0 |
4.若7x3y3与一个多项式的积是28x7y3-21x5y5+2y•(7x3y3)2,则这个多项式为( )
| A. | 4x4-3x2y2+14x3y4 | B. | 4x2y-3x2y2 | ||
| C. | 4x4-3y2 | D. | 4x4-3xy2+7xy3 |
1.已知点P(a,a+3)在抛物线y=x2-7x+19图象上,则点P关于原点O的对称点P′的坐标是( )
| A. | (4,7) | B. | (-4,-7) | C. | (4,-7) | D. | (-4,7) |
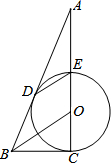 如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.
如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.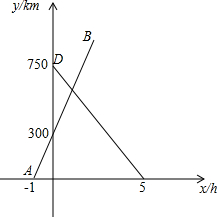 铁路中心记录途经南京的各型号列车行驶情况,如图,上午7:00为起始时间,列车x小时后距南京y千米,线段AB和DE分别表示一辆动车和一辆特快列车行驶过程中y与x的函数关系,点A坐标为(-1,0),点B坐标为(2,900).
铁路中心记录途经南京的各型号列车行驶情况,如图,上午7:00为起始时间,列车x小时后距南京y千米,线段AB和DE分别表示一辆动车和一辆特快列车行驶过程中y与x的函数关系,点A坐标为(-1,0),点B坐标为(2,900).